CASOPIS REPUBLICKE AGENCIJE ZA TELEKOMUNIKACIJE

SADRŽAJ

Detekcija ivica u slici je jedan od osnovnih koraka u interpretaciji sadržaja slike, možda i najvažniji. Za ispravnu detekciju svih ivica neophodan je multirezolucijski pristup, u kojem wavelet transformacija igra ključnu ulogu. Rad ukratko prikazuje dosadašnje doprinose u ovoj oblasti i predlaže novi, modifikovani algoritam baziran na množenju wavelet koeficijenata sa prve tri skale kao detektor ivica opšte namene. Na kraju je opisana i jedna od metodologija poređenja detektora ivica, čijim korišćenjem je dat uporedni prikaz predloženog algoritma i nekoliko algoritama koji se često sreću u literaturi.

1. UVOD

Interpretacija sadržaja slike predstavlja krajnji cilj kompjuterske vizije i jedan je od najznačajnijih i najčešćih zadataka obrade slike. Slika poseduje veliki broj informacija o snimljenoj sceni, kao što su broj i oblik objekata, njihova veličina, orijentacija, tekstura i drugo, tako da izdvajanje tih objekata iz pozadine predstavlja primarni zadatak koji se mora izvršiti pre finalne interpretacije [1]. U cilju izdvajanja konture objekta neophodno je odrediti ivice koje definišu taj objekat, i ta činjenica potvrđuje da detekcija ivica ima ključnu ulogu u kompjuterskoj viziji [2], što rezultuje objavljivanjem nekoliko novih detektora ivica godišnje [4].

Predstavljanje slike pomoću ivica objekata prisutnih u snimljenoj sceni drastično smanjuje količinu podataka koje je potrebno obraditi, zadržavajući ključne informacije o obliku objekta. Dobijene ivice objekata se mogu potom iskoristiti u algoritmima za prepoznavanje i klasifikaciju objekata. Najvažnija osobina detektora ivica je mogućnost izdvajanja ivice tamo gde ona zaista postoji, sa ispravnom orijentacijom i dobrom lokalizacijom. Međutim, i pored velikog broja postojećih detektora, ne postoji opšte prihvaćen parametar koji opisuje kvalitet ivica i često se poređenje vrši subjektivno i na osnovu aplikacije u kojoj se detektor ivica primenjuje [1].

Uopšteno, detekcija ivica se sastoji od tri koraka. U prvom koraku potrebno je maksimalno smanjiti šum u slici, kako bi se ostvarile što bolje performanse detektora, odnosno sprečili lažna detekcija nepostojećih ivica, izostanak detekcije pravih ivica i delokalizacija pozicije ivica objekata. Redukcija šuma se najčešće vrši niskopropusnim (low-pass) filtriranjem, jer šum predstavlja visokofrekvencijski signal. Međutim, uklanjanjem šuma gubi se i deo informacije o ivici objekta, jer i sama ivica predstavlja visokofrekvencijski signal i prelaz između objekta i pozadine će nakon filtriranja biti manje izražen. Drugi korak u detekciji ivica je visokopropusno filtriranje, najčešće realizovano pomoću diferenciranja, pri čemu deo signala koji nije uklonjen niskopropusnim filtriranjem predstavlja potencijalnu ivicu objekta. U trećem koraku potrebno je lokalizovati ivicu i ukloniti piksele koji su lažno detektovani kao ivični, jer proizvode sličan izlaz iz visokopropusnog filtra kao i ivični pikseli.

Niskopropusno filtriranje zahteva konstrukciju optimalnog filtra koji predstavlja kompromis između eliminacije šuma i očuvanja strukture ivice. Ivica se najčešće opisuje svojom skalom koja se može tumačiti kao širina ivice, odnosno deo u kome se javlja prelaz između dva uniformna regiona u slici. Uobičajeno je da filtar sadrži parametar koji određuje njegovu skalu, i u slučaju Gausovog filtra skala odgovara standardnoj devijaciji σ. Ukoliko širina ivice približno odgovara parametru σ, položaj ivice dobija se kao lokalni maksimum apsolutne vrednosti konvolucije signala sa prvim izvodom Gausovog filtra. Ukoliko se koristi drugi izvod, ivicu predstavlja prolazak kroz nulu (zero crossing) konvolucije signala sa drugim izvodom niskopropusnog filtra, najčešće Gausovog. Međutim, kako slika sadrži objekte različitih veličina i oblika ivica, pri čemu neki od njih mogu biti i van fokusa kamere, nemoguće je samo na jednoj skali detektovati sve potrebne ivice, što je ilustrovano na Slici 1.

Slika 1. Uticaj skale niskopropusnog filtra na veličinu objekta koji se želi detektovati [6].

Iako je za detekciju najvećeg broja ivica u slici neophodno analizirati sliku na nekoliko skala, prvi detektori ivica (u literaturi se nazivaju i klasični detektori) ne sadrže niskopropusni filtar za uklanjanje šuma, već se izvršava samo diferenciranje slike. Najpoznatiji su Sobel (1970. godina), Prewitt (1970), Kirsch (1971), Robinson (1977) i Frei–Chen (1977), nazvani po svojim autorima. Sobel i Prewitt detektori ivica procenjuju gradijent na osnovu maske 3x3, a piksel se proglašava za ivični ukoliko je gradijent veći od definisanog praga. Slični su Kirsch i Robinson detektori, koji koriste 8 maski, za svaki pravac po jednu. Frei–Chen detektor ivica koristi 9 maski i dodatno procesiranje koje ispoljava najbolje rezultate u odnosu na druge klasične detektore ivica [7], [8]. Ipak, Sobel detektor ivica je najpoznatiji i najpopularniji među klasičnim metodama, zbog svoje jednostavnije implementacije i boljih performansi pri detekciji dijagonalnih ivica u odnosu na Prewitt detektor [9]. Najveći problem klasičnih metoda detekcije ivica predstavlja njihova velika osetljivost na šum, jer ne sadrže korak niskopropusnog filtriranja. Međutim, oni koriste maske čiji se efekat može posmatrati kao razlika srednjih vrednosti piksela sa različitih strana ivice, što predstavlja vid niskopropusnog filtriranja. Ako bi se povećala površina koja se koristi za određivanje srednje vrednosti, uticaj šuma bi se umanjio. Ta ideja je korišćena kod realizacije klasičnih detektora ivica sa većim maskama. Veličina maske se menja od tačke do tačke slike. Za svaki piksel povećava se dimenzija maske sve dok naglo ne opadne izlazna vrednost detektora. Optimalna dimenzija maske za posmatrani piksel je dimenzija koja prethodi naglom padu izlazne vrednosti detektora. Predložene dimenzije detektora srazmerne su stepenu broja 2 [10]. Jasno je da je opisani postupak detekcije ivica nepraktičan za izvršavanje u realnom vremenu, ali predstavlja prvi korak u procesiranju slike na različitim skalama.

Ogroman doprinos u razvoju detektora ivica dali su Marr i Hildreth (1980) [11] i Canny (1986) [5]. Oba detektora su bazirana na Gausovom filtru, koji je, zbog svojih dobrih karakteristika, najzastupljeniji filtar u obradi slike [1]. U cilju detektovanja ivica Marr i Hildreth su predložili određivanje prolaska kroz nulu drugog izvoda u pravcu gradijenta. Utvrdili su da se varijacija intenziteta u slici javlja na različitim skalama, što zahteva upotrebu niskopropusnog filtra različitih standardnih odstupanja σ. Međutim, detekcija prolaska kroz nulu je pouzdan metod pronalaska ivice samo u slučaju velikog odnosa signal-šum. Javlja se i greška u lokalizaciji pozicije ivice koja je srazmerna standardnoj devijaciji filtra. Dodatni problem predstavlja i detekcija lažnih ivica, jer nula u drugom izvodu ukazuje i na maksimum i na minimum prvog izvoda, a ivica odgovara isključivo maksimumu apsolutne vrednosti prvog izvoda. U zavisnosti od odnosa signal-šum moguć je i nedostatak pojedinih pravih ivica u rezultujućoj slici. Ipak, performanse Marr i Hildreth detektora ivica su bolje u odnosu na klasične detektore [12].

Najpopularniji detektor ivica predložio je Canny [5] i njegov algoritam se i danas smatra standardnim algoritmom za detekciju ivica u industriji i ispoljava bolje performanse u odnosu na mnoge novije detektore ivica. Canny je detekciju ivica posmatrao kao optimizacioni problem. Razmatrao je tri kriterijuma koje bi detektor ivica trebalo da ispuni:

-ispravna detekcija, odnosno primena optimalnog filtra koja rezultuje velikim odnosom signal-šum,

-tačna lokalizacija ivice,

-samo jedan odziv za svaku pronađenu ivicu.

Filtar koji zadovoljava pomenuti kriterijume Canny je odredio varijacionim računom. Pokazao je da ne postoji analitičko rešenje, ali da se u slučaju 1D signala i odskočne ivice optimalni filtar može aproksimirati prvim izvodom Gausove funkcije. U slučaju 2D signala, Canny je predložio upotrebu dva filtra, jednog u pravcu x-ose i drugog u pravcu y-ose. Canny detektor određuje ivicu tražeći lokalne maksimume u pravcu gradijenta, a zatim se na kandidate primenjuje princip dvostrukog praga [12], kako bi se odbacile lažne ivice koju su posledica šuma. Opisana procedura može se primeniti i za pronalaženje ivica proizvoljnog profila [1], ali je uobičajena primena standardnog algoritma razvijenog za odskočnu ivicu [12] i on se i podrazumeva kada se koristi Canny detektor. Canny je predložio i šemu za kombinaciju rezultata detekcije ivica na različitim skalama.

Nedostatak Canny detektora predstavlja nemogućnost razlikovanja varijacija sive boje usled šuma ili nedovoljno izraženih ivica kada ne postoji dovoljno izražen prelaz između dve oblasti [3]. Ipak, najveći broj detektora razvijenih nakon pojave Canny-evog koriste ili Gausov filtar ili funkciju sličnu Gausovoj i njene izvode. Navedeno opravdava verovanje da se optimalan linearan filtar za detekciju ivica ne razlikuje značajno od Gausovog filtra i njegovih izvoda [1].

Iako su realizovani pre više od dve decenije, Canny i Marr–Hildreth detektori su i danas najzastupljeniji i smatraju se referentnim detektorima, zbog čega se najčešće i koriste pri ispitivanju performansi drugih detektora ivica.

Usledio je multirezolucijski pristup detekciji ivica koji se sastoji od ponovljenih detekcija ivica na nekoliko različitih skala primenom Gausovog filtra, u cilju postizanja željenih performansi. Najveći izazovi su izbor pravog skupa skala, sinteza rezultata detekcije ivica na različitim skalama i prilagođavanje na različite nivoe šuma u slici. Među prvima koji su se bavili ponašanjem signala na različitim skalama je Witkin [13]. Posmatrao je karakteristike 1D signala na različitim skalama nakon primene LoG filtra (Laplacian of Gaussian), prateći lokacije prolaska kroz nulu rezultata primene LoG filtra i zadržavajući one kod kojih se prolazak kroz nulu javlja na većem broju skala. Witkin-ov rad predstavlja osnovu za mnoge detektore ivica koji razmatraju sliku na različitim skalama, a koji su kasnije usledili [3]. Gothtasby je predložio algoritam koji koristi modifikovanu predstavu slike na različitim skalama [14]. Na svakoj skali beleži se znak posmatranog piksela nakon primene LoG filtra. Kada se odredi predstava slike na svim potrebnim skalama, započinje postupak praćenja ivica od najviše ka najnižoj skali. Nedostatak opisanog algoritma ogleda se u velikoj količini memorije koju zahteva pri izvršavanju. U cilju rešavanja problema sinteze rezultata detekcije ivica na različitim skalama, Jeong i Kim su predložili iterativni postupak u kome se određuje optimalna skala za svaki piksel u slici [15]. Nakon ovog postupka dobija se finalna mapa ivica primenom Canny ili Marr–Hildreth detektora, u odnosu na koje sam algoritam pokazuje nešto bolje performanse u slici sa različitim tipovima ivica. Međutim, rezultati drastično zavise od izbora početne vrednosti parametra i broja iteracija koji se koriste za određivanje optimalne vrednosti varijanse Gausovog filtra. Mana algoritma je i dugo vreme izvršavanja [3].

Savremene metode multirezolucijske detekcije ivica bazirane su na wavelet transformaciji, koja omogućava multirezolucijsku predstavu slike. Metode koriste tu osobinu wavelet transformacije da bi se istovremeno analizirala struktura slike na malim i velikim skalama, i da bi se kombinovale informacije o ivicama sa različitih skala. Koeficijenti wavelet transformacije realne slike su retki, tj. većina koeficijenata ima vrednost blisku nuli. Koeficijent wavelet transformacije ima veliku vrednost jedino ukoliko se unutar podrške (oblasti definisanosti) korišćene wavelet funkcije nađe ivica objekta.

Najjednostavniji metod detekcije ivica zasnovan na wavelet transformaciji sastoji se od primene nekoliko koraka direktne transformacije, brisanjem slike aproksimacija na krajnjoj skali (odnosno, njenom zamenom slikom istih dimenzija u kojoj su svi članovi nula), upotrebom inverzne transformacije i primenom praga na apsolutnu vrednost rezultujuće slike [12], što je prikazano na Slici 2. Transformacija prikazana na slikama 2.(b) i 2.(c) naziva se brza wavelet transformacije (fast wavelet transform – FWT). Ako je u pitanju neki drugi oblik wavelet transformacije to se naglašava.

Slika 2. (a) Početna slika. (b) FWT početne slike na dve skale. (c) IFWT (Inverzna FWT) slike (b) pri čemu je slika aproksimacija (1/16 slike (b) u gornjem levom uglu) obrisana [12]. (d) Mapa ivica.

Sličan postupak opisali su autori rada [16]. Aydin et al. [17] su predstavili detektor ivica zasnovan na wavelet transformaciji i prolasku drugog izvoda kroz nulu. Ideja autora ogleda se u činjenici da različitim oblicima ivica odgovaraju različite skale i orijentacije wavelet transformacije. Pokazano je da predloženi detektor ivica daje subjektivno bolje rezultate u odnosu na Canny i Marr-Hildreth detektore ivica, ali nije naveden način izbora parametara Canny i Marr-Hildreth detektora, koji imaju presudan uticaj na njihove performanse.

Većina detektora ivica bazirana na wavelet transformaciji polazi od ideja koje su prezentovali Mallat i Hwang [18], gde je detekcija ivice na svakoj skali transformacija realizovana kao u slučaju Canny detektora. Umesto izvoda Gausovog filtra na svakoj skali s se definišu dve wavelet funkcije, koje predstavljaju parcijalne izvode u x i y pravcu dvodimenzione funkcije skaliranja φ(x,y,s). Za svaki detektor potrebno je obezbediti mehanizam povezivanja ivica dobijenih na različitim skalama kako bi se dobila jedinstvena mapa ivica, pri čemu se mora uzeti u obzir da sa povećanjem skale dolazi do sve veće dislokacije pozicije ivice. Osim toga, potrebno je ispitati i uticaj šuma na nižim skalama. Kao rešenje predlaže se praćenje ponašanje modula wavelet transformacije na nekoliko sukscesivnih skala. Jedan postupak predložili su Ducottet et al. [19]. Polazeći od matematičkog modela tri tipa ivice: prelaz, vrh i linija, određen je način ponašanja modula wavelet transformacije sa porastom skale za svaki tip ivice. Za svaki potencijalni ivični piksel, prati se vrednost modula wavelet transformacije i linearnom regresijom određuju se parametri koji opisuju tip ivice i odgovarajuću skalu na kojoj će se izvršiti tačna lokalizacija ivice. Poređenje je izvršeno sa Canny detektorom i pokazano je da je predloženi algoritam superioran kada se koristi sintetička slika sa modelima ivica razmatranim u radu. Međutim, kod svakodnevnih slika, performanse su na strani Canny detektora. Nažalost, predloženi algoritam karakteriše i dugo vreme izvršavanja. Shin i Tseng [20] su predložili metod zasnovan na prostornom povezivanju detektovanih ivičnih piksela na najmanjoj skali, ukoliko postoji veza između njima odgovarajućih piksela na višoj skali wavelet transformacije.

Guo et al. su u [21] opisali algoritam koji kombinuje ivice detektovane na nekoliko skala, a potom se sinteza detektovanih ivičnih piksela određuje na osnovu težinske sume, čime je omogućeno da najveći doprinos ostvare ivice određene na srednjoj skali iz izabranog opsega. Što se tiče poređenja, izvršeno je samo vizuelno poređenje na osnovu jedne slike i ustanovljeno je da predloženi algoritam ostvaruje bolje performanse, posebno kada su objekti u slici na malom rastojanju.

Jednostavan algoritam baziran na proizvodu wavelet koeficijenata na dve susedne skale predložili su Zhang i Bao [22]. Autori polaze od činjenice da je ukupan broj maksimuma modula koji potiču od šuma na skali s = 2^j+1 dva puta manji u odnosu na prethodnu skalu s = 2^j. Nakon izračunavanja wavelet transformacija i množenja odgovarajućih koeficijenata za dve izabrane skale, primenjuje se standardni algoritam izbora modula maksimuma kao i kod Canny detektora. U odnosu na Canny detektor, ovaj detektor ispoljava bolje performanse, pri čemu je poređenje izvršeno na osnovu metodologije opisane u [9].

U cilju detekcije ivica koriste se i metode bazirane na statističkoj obradi signala, fazi logici, neuralnim mrežama i drugim principima, ali one nisu predmet ovog rada. Detalji o njima se nalaze u [1].

2. ALGORITAM

Furijeova transformacija je predstavljala osnovni alat za procesiranje slike u transformacionom domenu [12] sve do sredine 80-tih godina prošlog veka od kada wavelet transformacija zauzima to mesto, pre svega u kompresiji i prenosu, ali i analizi slike. Za razliku od Furijeove, kod wavelet transformacije bazne funkcije su vremenski ograničene, a frekvencija im se može proizvoljno menjati. Moguće je odrediti i vremenski interval u kome se javlja određeni frekvencijski sadržaj, što nije izvodljivo primenom Furijeove transformacije. Kako ivice predstavljaju naglu promenu u signalu, očigledna je prednost koji nudi wavelet transformacija. Za detalje o wavelet transformaciji pogledati [23].

Algoritam za detekciju ivica (u daljem tekstu DMW – detektor ivica baziran na množenju koeficijenata wavelet transformacije) opisan u [26] zasnovan je na jednom obliku transformacije koja se u literaturi susreće pod nazivom“algorithme à trous” [23], a poznata je i pod drugim nazivima: redundantna, stacionarna, bez decimacije, itd, [24]. Operacija decimacije kod FWT dovodi do translacije ivica, što je nepoželjno u algoritmima za prepoznavanje i klasifikaciju objekata [25], jer rezultat zavisi od toga da li će se zadržati parni ili neparni članovi niza [24]. Redundantna wavelet transformacija generiše isti broj koeficijenata na svakoj skali, jednak broju članova početnog niza. Kao rezultat postoji jednostavna prostorna veza između wavelet koeficijenata na različitim skalama.

DMW je zasnovan na idejama predloženim u [22] i detaljno je razmatran u [26]. Međutim, za razliku od originalne ideje, umesto da se koriste koeficijenti sa dve susedne skale, međusobno su pomnoženi koeficijenti sa tri skale wavelet transformacije originalne slike. Naime, DMW je realizovan za inspekciju kvaliteta kartona u procesu njegove proizvodnje i pronalaženju defekata na kartonu. Kao takav, prilagođen je detekciji ivica defekata u slikama kartona uz znatno prisustvo šuma [26]. U tim uslovima množenje koeficijenata sa tri skale daje bolje rezultate od množenja sa dve skale, što se može uočiti i na Slici 3.

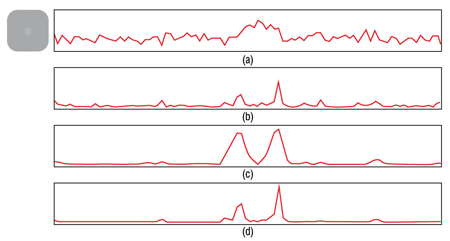
Slika 3. (a) Slika defekta na kartonu i horizontalni profil sive duž defekta. Proizvod koeficijenata detalja 1D wavelet transformacija za profil prikazan na slici (a) sa: (b) I i II, (c) II i III, (d) sve tri skale.

Slično kao i u radu [22], vrednost gradijenta Mf(x,y) u posmatranoj tački slike (x,y), određuje se na osnovu izraza:

gde je proizvod wavelet koeficijenata za horizontalne i = 1 i vertikalne i = 2 detalje. Pravac gradijenta Af(x,y) određuje se pomoću formule [2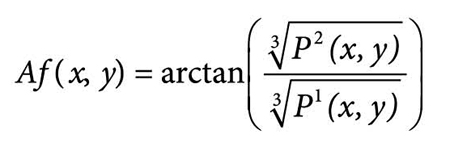2]:

(2)

Pokazano je da DMW ispoljava bolje performanse pri detekciji ivica defekata na kartonu u odnosu na Canny detektor ivica [26]. Dobijeni rezultat je očekivan, jer ako je detektor ivica projektovan za specifičan problem, njegove karakteristike na ciljanom tipu slika su bolje u odnosu na druge detektore [27].

Detektor koji se razmatra u ovom radu (u daljem tekstu DMW2) je modifikovana verzija detektora DMW. Izvršena je zamenom biortogonalnog wavelet-a bior3.1 (koji se najbolje pokazao na slikama kartona) haar wavelet-om, jer je za svakodnevne slike ustanovljeno da haar wavelet tačnije i kompletnije pronalazi ivice [20].

Najbolja lokalizacija ivice ostvaruje se na najmanjoj skali i samo koeficijenti sa prve skale se mogu iskoristiti za računanje gradijenta. Tada se izraz (2) modifikuje u sledeću formulu:

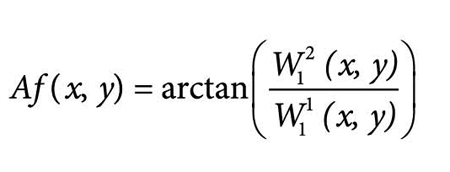(3)

što omogućava da DMW2 istovremeno zadrži osobine potiskivanja šuma množenjem koeficijenata na tri uzastopne skale wavelet transformacija i dobru lokalizaciju ivica koja se ostvaruje na najnižoj skali. Nakon zadržavanja samo onih vrednosti gradijenta Mf(x,y) za koje se dostiže lokalni maksimum u pravcu gradijenta, datim izrazom (3) pristupa se dvostrukom pragu. Ukoliko je Mf(x,y) > t_high (t_high je gornji prag), tačka (x,y) proglašava se za ivični piksel, a ako važi relacija t_low < Mf(x,y) ≤ t_high, tačka (x,y) predstavlja potencijalni ivični piksel. Zatim se ispituju svi potencijalni ivični pikseli, a svaki potencijalni ivični piksel za koji se može ostvariti veza do ivičnog piksela, postaje i sam ivični. Dvostruki prag sprečava prekidanje konture, jer nije ivica u svim tačkama podjednako izražena, najčešće zbog neuniformnog osvetljenja ili zbog toga što se nalazi u senci drugih objekata. Ako bi se primenila samo jedna vrednost praga za koju su sve konture celovite, zbog šuma bi se pojavio veliki broj lažno detektovanih ivičnih piksela. Uvođenje dvostrukog praga kako bi se ostvarile bolje karakteristike pri obradi svakodnevnih slika predstavlja dodatnu modifikaciju DMW2 u odnosu na DMW.

3. TESTIRANJE PREDLOŽENOG ALGORITMA

Metodologija koja je korišćena za poređenje performansi detektora ivica predložena je u [28], a izabrana je kao najcitiranija metoda u ovoj oblasti. U literaturi se često sreće i postupak opisan u [9], međutim on je zasnovan samo na rezultatima dobijenim pomoću jedne kompjuterski generisane slike. Iz tog razloga, navedeni postupak se smatra nedovoljnim, jer se detektori ivica koriste za obradu slika dobijenih pomoću kamera ili skenera, u kojima nije unapred poznat tačan položaj objekata. Takođe, ako je detektor razvijen samo za jedan model ivica, očekivano je da daje dobre rezultate ako se primeni na veštački generisanoj slici koja sadrži korišćeni model ivice.

Metodologija poređenja detektora ivica je zasnovana na određivanju ROC krive za svaki od detektora. Slične metode opisane su u [27] i [29]. Procedura se sastoji od proračuna ROC (Receiver Operating Characteristic) krive za svaki od detektora koji se testira i smatra se da detektor sa najmanjom površinom ispod krive (AUC – area under the curve) pruža najbolje performanse. Poređenje DMW2 izvršeno je sa Canny detektorom, jer se on smatra referentnim, predstavlja industrijski standard, a pokazao je i zadovoljavajuće rezultate, kao i sa Marr-Hildreth detektorom. Sobel detektor je uključen u ispitivanje kao najčešće korišćeni klasični tip detektora ivica. U eksperiment je uključen i SUSAN (Smallest Univalue Segment Assimilating Nucleus) detektor ivica, koga karakteriše velika brzina izvršavanja i jednostavna implementacija. Za razliku od drugih detektora koji su zasnovani na diferenciranju, SUSAN detektor ispituje sličnosti između centralnog piksela u maski i okolnih piksela. Za centralni piksel formira se težinska suma i poredi se sa zadatim pragom. Ukoliko je težinska suma veća od zadatog praga, ispituje se da li centralni piksel predstavlja i lokalni maksimum. U pozitivnom slučaju, proglašava se za ivični piksel.

Za testiranje je korišćena baza slika koju su obezbedili autori metodologije na svom veb sajtu. Svaka slika poseduje odgovarajuću mapu ivica GT (Ground Truth). Kriterijum određivanja ispravnog poklapanja ivičnog piksela TP (True Positive) je sledeći: ukoliko detektor pronađe ivični piksel na lokaciji crnog piksela u GT slici sa dozvoljenom tolerancijom, proglašava se za TP. Tolerancija je maksimalno dozvoljeno rastojanje između pozicije pronađenog ivičnog piksela i odgovarajućeg piksela u GT slici. Uobičajeno je da ova vrednost iznosi 3 piksela. Ako detektor pronađe ivični piksel u zabranjenoj zoni (siva u GT slici) broj FP (False Positive) se uveličava za 1. Postoji i mogućnost detekcije ivičnog piksela u nemarkiranoj zoni (bela oblast u GT slici), što nema uticaja ni na broj TP ni na broj FP. Procenat TP i FP se određuje kao odnos dobijenih brojeva sa ukupnim brojem ivičnih piksela u GT slici (suma crnih piksela), odnosno svim nedozvoljenim površinama (suma sivih piksela). Na Slici 4. prikazane su jedna svakodnevna slika i njena odgovarajuća mapa ivica.

Slika 4. (a) Test slika i (b) odgovarajuća mapa ivica.

Iz skupa od 50 ponuđenih slika različitih objekata iz svakodnevnih prizora, slučajno je izabrano 15. Za svaku sliku, detektor se prvo trenira, što se postiže adaptivnim deljenjem intervala za skup vrednosti svakog od parametara. Svi detektori imaju po dva promenljiva parametra, osim Canny detektora koji poseduje tri. U prvom koraku opseg svakog parametra se deli u 4 tačke i za sve kombinacije se određuje rezultat (TP,FP). Autori metodologije [28] su predložili formiranje ROC krivih pomoću tačke (1–TP,FP), Slika 5. Tada 1–TP predstavlja procenat nedetektovanih ivičnih piksela i rezultat je bolji ako je površina ispod ROC krive manja. U sledećem koraku, u skup vrednosti svakog parametra ubacuju se tačke između svake dve vrednosti i određuje novi (TP,FP) par. Treniranje se završava kada promena površine ispod ROC krive između dve iteracije bude manja od 5%. Dobijeni skup parametara za posmatranu sliku se sada primenjuje na ostale slike iz skupa i određuje se ROC kriva za svaku od slika. Kao rezultat dobija se skup od 15 x 14, odnosno 210 ROC krivih. Pomoću 210 ROC krivih formira se agregatna ROC kriva i površina ispod nje, AUC, predstavlja ocenu performansi detektora.

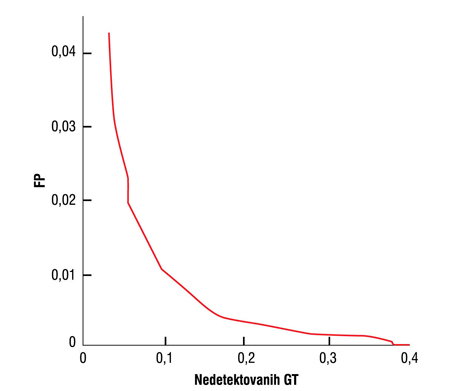
Slika 5. ROC kriva dobijena pri treniranja Canny detektora ivica na Slici 4a.

Za pojedine detektore, velika vrednost TP, veća od 95%, može se dobiti samo pri vrednosti FP od preko 25%, što je prikazano na Slici 6. Pri vrednosti TP = 98,45% Canny detektor prijavljuje vrednost FP = 26,89%, pri čemu je rezultat neupotrebljiv, Slika 6c. S druge strane, DMW2 daje rezultat (TP = 95,32%, FP = 0,33%) i ivice se pronalaze samo u očekivanim oblastima, Slika 6d. Opisano pokazuje da sama velika vrednost TP ne govori dovoljno o kvalitetu detektora.

Slika 6. (a) Test slika. (b) Odgovarajuća mapa ivica.

(c) Rezultat primene Canny detektora na sliku 6(a).

(d) Ivice pronađene predloženim algoritmom.

Na Slici 7. su prikazane agregatne ROC krive za sve navedene detektore, dok su u Tabeli 1. navedene njihove AUC vrednosti.

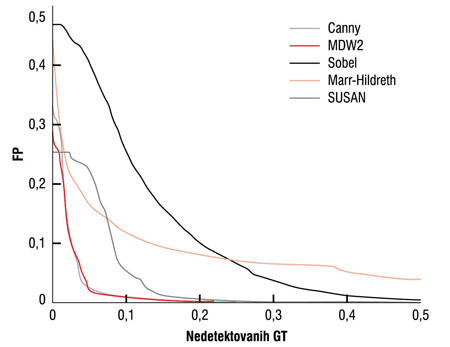
Slika 7. ROC krive za testirane detektore ivica.

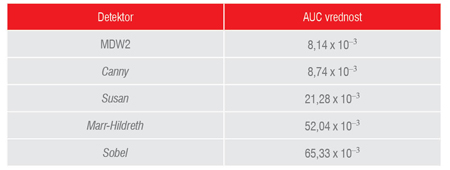
Tabela 1. AUC vrednosti za testirane detektore.

Na osnovu dobijenih rezultata može se zaključiti da najlošije performanse ispoljava Sobel detektor ivica, što je i očekivano zbog jednostavne konstrukcije. Sledi Marr-Hildreth detektor, dok se u sredini nalazi SUSAN detektor ivica. Značajno bolje performanse u odnosu na ostale ispoljavaju i DMW2 i Canny, a međusobno su uporedivi. Dobijena vrednost AUC je za 7% manja kod DMW2 u odnosu na Canny detektor ivica, odnosno DMW2 je neznatno bolji detektor ivica nego Canny.

Ipak, pri velikim vrednostima parametra TP, DMW2 detektor ivica prijavljuje mnogo manji broj lažno detektovanih ivičnih piksela.

4. ZAKLJUČAK

U radu je objašnjen princip detekcije ivica množenjem koeficijenata wavelet transformacije sa nekoliko uzastopnih skala i prikazan je detektor ivica (DMW) baziran na pomenutom principu, koji je prvenstveno bio razvijen za tipski problem detekcije ivica defekata na kartonu. Manjim modifikacijama DMW je unapređen i upotrebljen za detekciju ivica u svakodnevnim slikama. Data je metodologija upoređivanja performansi detektora ivica na osnovu ROC krive, pri čemu se u eksperimentu koriste realne slike. Za eksperimentalne potrebe realizovana je i biblioteka funkcija u programskom paketu Matlab. Eksperimentom je utvrđeno da su performanse DMW2 uporedive, čak i nešto bolje, od Canny detektora ivica, odnosno i DMW2 se može koristiti kao detektor opšte namene. U odnosno na ostala tri ispitivana detektora (Sobel, Marr-Hildreth i SUSAN), DMW2 ispoljava višestruko bolje karakteristike. Dodatno, za razliku od Canny detektora, pri detekciji velikog procenta očekivanih ivičnih piksela, DMW2 ostvaruje znatno manji broj lažno detektovanih ivica.

Literatura

[1] M. A. Oskoei, H. Hu, “A Survey on Edge Detection Methods”, Technical Report: CES-506, University of Essex, UK, 2010.
[2] W. Cao, R. Che, D. Ye, “An illumination-independent edge detection and fuzzy enhancement algorithm based on wavelet transform for non-uniform weak illumination images”, Pattern Recognition Letters, vol. 29, pp.192-199, 2008.
[3] M. Basu, “Gaussian-based edge-detection methods-a survey”, IEEE Transactions on Systems, Man and Cybernetics, Part C (Applications and Reviews), vol. 32, pp. 252-260, 2002.
[4] N. Senthilkumaran, R. Rajesh, “Edge Detection Techniques for Image Segmentation – A Survey of Soft Computing Approaches”, International Journal of Recent Trends in Engineering, vol. 1, pp. 250-254 2009.
[5] J. Canny, “A computational approach to edge detection”, IEEE Trans. on Pattern Analysis and Machine Intelligence, vol. 8, pp. 679-698, 1986.
[6] http://www.csc.kth.se/~tony/cern-review/cern-html/node2.html.
[7] W. Frei, C. C. Chen, “Fast Boundary Detection: A Generalization and a New Algorithm”, IEEE Trans. on Computers, vol. 26, pp 988 – 998, 1977.
[8] J. C. Russ, “The Image Processing Handbook”, CRC Press, 2002.
[9] W. K. Pratt, “Digital Image Processing”, John Wiley & Sons, 2007.
[10] A. J. Pinho, L. B. Almeida, “A review on edge detection based on filtering and differentiation”, Revista do Detua, vol. 2, pp. 113-126, 1997.
[11] D. Marr, E. Hildreth, “Theory of edge detection”, Proc. of the Royal Society of London. Series B, Biological Sciences, vol. 207, pp 187-217 , 1980.
[12] R. C. Gonzalez, R.E. Woods, “Digital Image Processing”, Prentice Hall, 2008.
[13] A. P. Witkin, “Scale-space filtering”, Proc. Intern. Joint Conference on Artificial Intelligence, vol. 2, pp. 1019-1022, 1983.
[14] A. Goshtasby, “On edge focusing”, Image and Vision Computing, vol. 12, pp. 247-256, 1994.
[15] H. Jeong, C. I. Kim, “Adaptive determination of filter scales for edge-detection”, IEEE Trans. on Pattern Analysis and Machine Intelligence, vol. 14, pp 579 - 585, 1992.
[16] L. Feng, C. Y. Suen, “Edge Extraction of Images by Reconstruction using Wavelet Decomposition Details at Different Resolution Levels”, International Journal of Pattern Recognition and Artificial Intelligence, vol. 14, pp. 779-793, 2000.
[17] T. Aydin, Y. Yemez, E. Anarim, B Sankur, “Multidirectional and multiscale edge detection via M-band wavelet transform”, IEEE Transactions on Image Processing, vol. 5, pp. 1370 - 1377, 1996.
[18] S. Mallat, W. L. Hwang, “Singularity Detection and Processing with Wavelets”, IEEE Transactions on Information Theory, vol. 38, pp. 617 – 643, 1992.
[19] C. Ducottet, T. Fournel. C. Barat, “Scale-adaptive detection and local characterization of edges based on wavelet transform”, Signal Processing, vol. 84, pp. 2115-2137, 2004.
[20] M. Shih, D. Tseng, “A wavelet-based multiresolution edge detection and tracking”, Image and Vision Computing, vol. 23, pp. 441-451, 2005.
[21] F. Guo, Y. Yang, B. Chen, L. Guo, “A novel multi-scale edge detection technique based on wavelet analysis with application in multiphase flows”, Powder Technology, vol. 202, pp. 171-177, 2010.
[22] L. Zhang and P. Bao, “Edge detection by scale multiplication in wavelet domain”, Pattern Recognition Letters, vol. 23, pp. 1771-1784, 2002.
[23] S. Mallat, “A Wavelet Tour of Signal Processing”, Academic Press, 2008.
[24] P. S. Adisson, “The Illustrated Wavelet Transform Handbook”, IOP Publishing Ltd, 2002.
[25] X. Yang, G. Pang and N. Yung, “Robust fabric defect detection and classification using multiple adaptive wavelets”, IEE Proc. - Vision, Image & Signal Processing vol. 6 pp. 715-723, 2005.
[26] M. Barjaktarovic, S. Petricevic, “Wavelet Based Edge Detection Algorithm for Web Surface Inspection of Coated Board Web”, Journal of Instrumentation, vol. 5, P07001, 2010.
[27] M. Heath, S. Sarkar, T. Sanocki, K. Bowyery, “Comparison of Edge Detectors – A Methodology and Initial Study”, Computer Vision and Image Understanding, vol. 69, pp. 38-54, 1998.
[28] K. Bowyer, C. Kranenburg, S. Dougherty, “Edge Detector Evaluation Using Empirical ROC curves”, Computer Vision and Image Understanding, vol. 84, pp, 77-103, 2001.
[29] M. C. Shin, “Comparison of Edge Detector Performance through Use in an Object Recognition Task”, Computer Vision and Image Understanding vol. 84, pp. 160–178, 2001.
[30] S. Smith, M. Brady, “SUSAN – A new approach to low level image processing”, Internat. J. Comput. Vision, vol. 23, pp. 45–78, 1997.

Autor

Marko Barjaktarović je diplomirao i magistrirao na Elektrotehničkom fakultetu Univerziteta u Beogradu gde je trenutno zaposlen u zvanju asistenta. Oblasti interesovanja autora su instrumentacija i digitalna obrada slike iz koje je objavio nekoliko stručnih i naučnih radova.