CASOPIS REPUBLICKE AGENCIJE ZA TELEKOMUNIKACIJE

SADRŽAJ

U tržišnom okruženju gde se korisnicima nude sve kompleksniji servisi potreba za racionalnom i optimalnom upotrebom resursa postaje sve izraženija. Ovo je posebno naglašeno kod prenosa multimedijalnih signala u realnom vremenu. Jedan od servisa koji nailazi na sve veće interesovanje je video konferencija gde više autorizovanih korisnika međusobno razmenjuje video i audio signale. Kako paket informacija od jednog korisnika treba da stigne do svih drugih, multicast rutiranje predstavlja optimalno iskorišćenje resursa mreže. Dinamičko rutiranje nameće dodatne uslove i restrikcije sa aspekta kvaliteta servisa. Dozvoljavanjem proizvoljnom broju korisnika da se uključi ili napusti video konferenciju, sa proizvoljnim trajanjem konekcije, ali garantovanim kvalitetom prenosa, proces rutiranja se izuzetno usložnjava. Imajući u vidu da logika rutiranja treba da „razmotri“ trenutno stanje u mreži (kapacitete linkova i trenutne gustine saobraćaja na njima), cene prenosa i kašnjenje signala (cele putanje, pojedinih deonica ili varijacije kašnjenja) nameće se potreba za inteligentnim rešenjima. Kao jedan od dokazanih kandidata su i neuralne mreže. S obzirom da se u problemu dinamičkog multicast rutiranja razmatra optimizacija više različitih parametara kao model neuralne mreže u ovom radu će se upotrebiti Hopfildova neuralna mreža (Hopfield Neural Network). Razvijen je algoritam i softverski alat za potrebe multicast rutiranja koji u obzir uzima kapacitet linkova, gustinu saobraćaja, cenu prenosa po linkovima i kašnjenje na pojedinim deonicama. Cilj softverskog alata je pronalaženje Pareto optimalne putanje za rutiranje paketa.

Ključne reči — Dinamičko rutiranje, multicast, Steiner tree problem, Hopfildova neuralna mreža, video konferencija.

1. UVOD

Problem rutiranja sve više dobija na značaju sa razvojem savremenih računarskih mreža. Opšta tendencija eksponencijalnog rasta broja korisnika ovih mreža, i sve veći zahtevi za prenosom informacija, povećavaju i broj kompanija koje se bave pružanjem usluga. Uporedo sa njima raste i potreba za opremom koja je u mogućnosti da zadovolji složene procese rutiranja, kako interne komunikacije potrebne za rad sistema, tako i paketa informacija koji se prenose [1].

Najčešće korišćeni algoritam za rutiranje je Dajkstra (Dijkstra), ali se uporedo sa njegovom implementacijom pokušavaju razviti novi i bolji algoritmi [2]. Da bi razdvojili problem rutiranja na dve podoblasti, veliki proizvođači najčešće razdvajaju problem traženja optimalne metrike, po kojoj će se vršiti proces rutiranja, i algoritme koji na osnovu metrika treba da pronađu Pareto optimalne putanje.

Optimizacija procesa rutiranja i adekvatna metrika posebno dolaze do izražaja kada korisnici imaju visoke zahteve sa aspekta kvaliteta servisa i njihove cene. Sa jedne strane se pojavljuju sadržaji namenjeni zabavi (video-on-demand, news-on-demand, masovno slanje mail-ova itd.) ali i komercijalnim primenama (video konferencije, telemedicina, distribuirane baze podataka, itd.) koji zahtevaju relativno velike resurse ili njihovu optimalnu upotrebu [3- 6].

Kod većine savremenih servisa postoji potreba da se do sada najzastupljenije rutiranje point-to-point zameni multicast rutiranjem koje sa sobom donosi nove servise [7]. Razvojem tehnološkog društva, a u skladu sa savremenim poslovnim tendencijama, novi dinamički servisi su atraktivni ali i pogodni korisnicima zbog niske cene i mogućnosti upotrebe istih bez nadogradnje ili zamene postojeće opreme.

Dinamičko rutiranje nosi i problem koji se najteže može tačno opisati matematičkim relacijama, a to je definisanje trenutka konektovanja korisnika na mrežu ili grupu kojoj pripada. Ovaj problem se može sagledati kroz lokaciju gde se korisnik priključuje i dužinu vremena koje će korisnik provesti u multicast grupi.

Generalno gledano postoje tri opšta uslova koje je potrebno zadovoljiti kod dinamičkog multicast rutiranja, pa samim tim i njegove implementacije. To su kašnjenje signala, varijacija u kašnjenju i kapaciteti linka [8-9]. Kašnjenje signala se može posmatrati kao suma kašnjenja svih linkova po kojima se zatvara putanja ili kao poseban uslov kojim se u metrici linkovi sa manjim kašnjenjem „stimulišu“ da se nađu u krajnjem rešenju, tj. linkovi sa kašnjenjem preko tačno definisane vrednosti zabranjuju.

U literaturi postoje rešenja koja deo ovih problema rešavaju različitim metodama [9-11]. Ovaj rad predstavlja jedno rešenje za multicast rutiranje koje se bavi paralelnom optimizacijom ukupne cene Štajnerovog stabla (Steiner tree), ali i minimizacijom ukupne cene sa aspekta broja hopova, dužine putanja u stablu, zagušenja i kašnjenja na pojedinačnim linkovima. Zagušenje se analizira razmatranjem kapaciteta linka i trenutnog saobraćaja po svakom od njih, u skladu sa definisanim kvalitetom servisa.

2. MATEMATIČKI MODEL: ŠTAJNEROVO STABLO

Neka je dat težinski graf G=(V,E) gde su V čvorovi a E grane (linkovi) tog grafa. Neka je za takav graf definisan podskup D Í V. Štajnerovo stablo (Steiner tree) je stablo u grafu G koje spaja sve čvorove u D={d₁,d₂,...,d_K}. Dodatnom restrikcijom definiše se i minimalno Štajnerovo stablo (Minimum Steiner tree in graph - MStTG) kao stablo za koje je ukupno rastojanje na njegovim granama minimalna vrednost među svim mogućim Štajnerovim stablima za dato G i D. U takvom stablu postoji mogućnost da se koriste čvorovi D¢={d₁,d₂,...,d_K,...d_K¢}, gde je D¢Ê D. Čvorovi koji su elementi (D¢-D) se nazivaju Štajnerovi čvorovi [12].

Problem pronalaženja Štajnerovog stabla spada u „NP-complete“, i algoritmi za njegovo izračunavanje datiraju od sedamdesetih godina prošlog veka [13]. Uvođenjem ograničenja u smislu kvaliteta servisa, a naročito kada se radi o prenosu zahtevnih video signala u realnom vremenu dobijaju se Constrained Minimum Steiner Tree in Graph (CMStTG). Ova ograničenja odnose se na kašnjenje u prenosu, varijacije u kašnjenju i propusni opseg [14].

2.1. Modifikacija i definisanje problema dinamičkog multicast rutiranja

Polazeći od funkcije iz rada [15], i uvođenjem pojma kašnjenja po linku realizovan je model za dinamičko multicast rutiranje. Ovaj model traži MStTG u zadatom grafu sa ciljem minimizacije opšte cene težinskog grafa. Svaki od linkova je opisan svojom inicijalnom cenom (koja može biti fizičko rastojanje, tj. indirektno izračunato vreme prenosa kroz posmatranu deonicu, ili stvarna cena prenosa po jedinici dužine), kapacitetom, trenutnom gustinom saobraćaja i kašnjenjem. Cilj je pronalaženje Pareto optimalne putanje koja može da odgovori potrebama promena konfiguracije grafa, u smislu konektovanja novih korisnika, i obezbedi minimalno odbacivanje paketa usled zagušenosti linka [15-16].

3. VEŠTAČKE NEURALNE MREŽE

Veštačke neuralne mreže predstavljaju relativno novu paradigmu neanalitičkog rešavanja problema, koja se, zahvaljujući svojim mogućnostima, primenjuje u različitim oblastima. U osnovi se pokušava napraviti veštački sistem, inspirisan biološkim nervnim sistemom, koji je sposoban da uči i donosi inteligentne odluke bez precizno utvrđenog algoritma. Mada je rad pojedinačnih neurona spor, kompletna neuralna mreža radi veoma brzo (kaže se „brz kao misao“) što je posledica velike povezanosti neurona i paralelnog procesiranja. Građa nervnog sistema i elektrohemijski procesi u mozgu su veoma dobro istraženi, mada su mehanizmi viših moždanih procesa (procesi mišljenja i donošenja logičkih zaključaka) još uvek nedovoljno istraženi. Stoga pokušaji kompletne simulacije i praćenja procesa rada biološkog nervnog sistema predstavljaju veoma kompleksan zadatak. Na sreću, veliki broj složenih procesa se može, u nekim slučajevima, razložiti na niz manje kompleksnih problema, što se koristi i u realizacijama veštačkih neuralnih mreža. Pored neuralnih mreža, postoje još neki napredni sistemi koji imaju svojstvo da rešavaju probleme na osnovu nedovoljno čvrsto postavljenih pravila. Najpoznatiji su genetski algoritmi, fazi logika, adaptivne memorije, asocijativne memorije i slično, ali su se neuralne mreže do sada pokazale najprihvatljivijim i najadaptivnijim [17].

Osnovni rival neuralnim mrežama je klasični računarski program. Razlike između ova dva sistema su izuzetno velike. Konvencionalni računari rade na logičkoj osnovi, sekvencijalno, deterministički ili sa vrlo niskim stepenom paralelizma. Problemi se rešavaju u centralnoj procesorskoj jedinici (ili više njih) na bazi precizno definisanog algoritma (programa) koji se kreira za rešavanje datog problema. Ovi programi zahtevaju promenu svaki put kada se tip problema ili okruženja minimalno promeni. Promene su skupe, i u zavisnosti od problema i dugotrajne. Podaci se čuvaju u centralnoj memorijskoj jedinici (ili u više njih) i pozivaju se iz centralne procesorske jedinice po potrebi. Rešavanje problema se vrši numerički, sinhronizovano centralnim generatorom takta, i sekvencijalno, korak po korak, često uz višestruko ponavljanje istih operacija, tako da je vreme procesiranja često veoma dugo, mada su brzine takta današnjih računara veoma velike (reda 10 GHz). Takođe, otkaz bilo kog dela sistema dovodi do prekida rada sistema.

Neuralne mreže sadrže veliki broj prostih procesirajućih jedinica (neurona) a obrada i arhiviranje podataka su distribuirani (raspodeljeni po svim neuronima), dok je rad mreže paralelan. Usled masovnog paralelizma rešavanje problema je veoma brzo, reda veličine nekoliko vremenskih konstanti neurona (što je reda veličine ms ili ns), i nezavisno od složenosti problema. Osnovna karakteristika veštačkih neuralnih mreža je da one ne rade po utvrđenom programu već su sposobne da uče na osnovu primera. Jednom obučena mreža je u stanju da rešava niz problema sličnih onima koji su se koristili prilikom obučavanja. Mreža je fleksibilna i relativno malo osetljiva na ispad izvesnog broja neurona. Sama se prilagođava promenama i stanjima koje uči. Mreža je vrlo imuna na najveći od problema savremenih sistema - šum. Svaki memorijski element je delokalizovan - raspodeljen je po celoj mreži.

3.1. Hopfildova neuralna mreža

Posebnu vrstu neuralnih mreža predstavljaju rekurentne neuralne mreže. Ove mreže se karakterišu povratnom vezom izlaznog sloja neurona ka ulaznom, pri čemu se nad tim signalom može izvršiti neka modifikacija. Najčešće je to vremensko kašnjenje signala. Kao predstavnik ovih mreža najčešće se uzima Hopfildova neuralna mreža [18], čija struktura je prikazana na slici 1.

Najčešća upotreba Hopfildove neuralne mreže je u problemima optimizacije [19-21]. Najpoznatiji problem ove vrste je problem trgovačkog putnika (TSP - Traveling Salesman Problem) koji je preuzet iz teorije grafova, i vrlo brzo, zahvaljujući svojoj složenosti, postao mera kvaliteta nekog optimizacionog algoritma.

Hopfildova neuralna mreža se pokazala kao dobar alat za rešavanje ovakve vrste problema [18],[22], [23] čime je privukla veliki broj istraživača u cilju rešavanja ostalih optimizacionih problema.

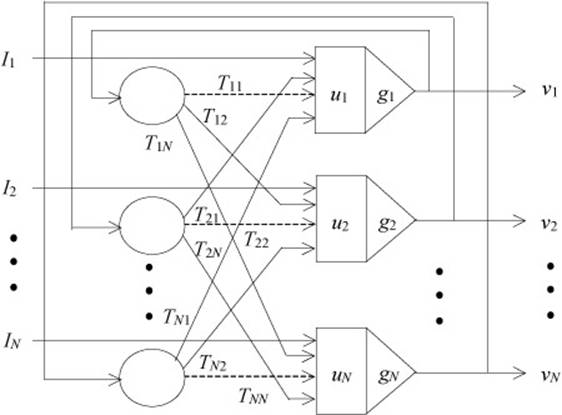
Slika 1. Struktura Hopfildove neuralne mreže

Mreža je dizajnirana po modelu klasičnih rekurentnih mreža [24]. Svaki od neurona realizovan je kao operacioni pojačavač sa sigmoidalno rastućom funkcijom koja povezuje izlaz V_i i ulaz U_i i-tog neurona. Na ovaj način mreža dobija karakteristiku nelinearnosti. Izlazne vrednosti su skalirane na opseg od 0 do 1. Funkcija prenosa (aktivaciona funkcija) za svaki od neurona data je kao [18], [25]

(1)

gde je a konstanta koja određuje nagib karakteristike.

Shodno pravilu rekurzivnih mreža, izlazni signal i-tog neurona vodi se na sve ulaze drugih neurona sem na sopstveni ulaz, preko rezistivnih veza. Ova povezanost definisana je matricom povezanosti T=[T_ij]. Pored signala koji prima od izlaznih neurona, na svaki od ulaznih neurona deluje dodatni strujni signal (bias current) I_i. Njime se podešava polarizacija neurona. Promene ulaznih signala su definisane relacijom (2), slika 1,

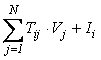= - + (2)

gde je τ vremenska konstanta.

Moguća realizacija Hopfildove ćelije data je da slici 2. Izlazi neurona, V_j, se preko otpornika R_ij stiču na kondenzator C_i,. Promena napona na kondenzatoru data je jednačinom stanja [25], [26].

. (3)

Napon kondenzatora C_i deluje na ulazu nelinearnog diferencijalnog pojačavača, na čijem izlazu se dobijaju signali V_i i -V_i ove ćelije, prema relaciji (1) [21], [26].

Hopfild je pokazao da će u slučaju da je pojačanje pojačavača relativno veliko (teoretski a→∞, kada je prenosna funkcija (1) odskočna) energijska funkcija biti [18], [28]

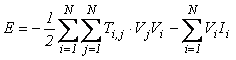(4)

Za veliko pojačanje operacionog pojačavača, minimum energije u datom N dimenzionalnom prostoru se raspoređuje u 2^N rogljeva. Tada se dinamika i-tog neurona, shodno relaciji (2), može prikazati kao [18]

= - - (5)

Relacija (5) definiše promenu ulaznog signala i promenu energije, u svakoj od iteracija. Može se pokazati da ovako definisana mreža obezbeđuje konvergenciju ka stabilnim stanjima [29]. Ovako postavljena mreža služi kao osnovna struktura za rešavanje optimizacionih problema.

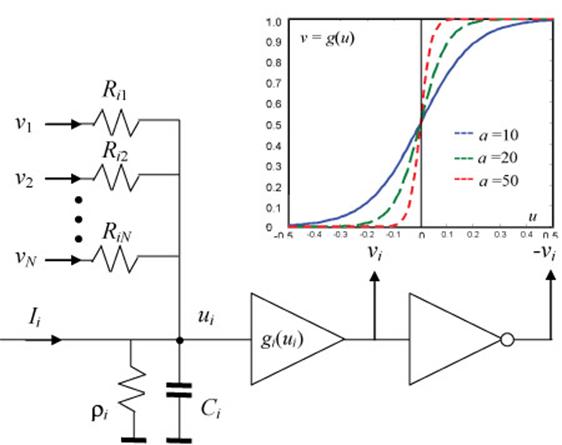
Slika 2. Realizacija neurona Hopfildove neuralne mreže pomoću elektronskih komponenti

Svaki konkretan problem dodatno koriguje energijsku funkciju, a samim tim i dinamiku ulaznih neurona. Jedan od takvih je i izbor najkraće putanje između dva čvora u mreži [30], [31].

3.2. Predloženi model Hopfildove neuralne mreže

Ulazni parametri Hopfildove mreže namenjene rešavanju problema rutiranja u telekomunikacionoj mreži su matrica cena (C), matrica kapaciteta linkova (K), gustina saobraćaja na njima (G) i kašnjenja po linkovima T [32]. Vrednosti ovih matrica mogu ali i ne moraju biti simetrične u odnosu na glavnu dijagonalu, čime se dobijaju bidirekcioni linkovi sa različitim mrežnim parametrima [30-31]. Matrica ρ koja definiše povezanost čvorova u mreži definisana je kao:

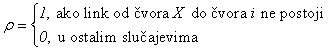
Za razliku od point-to-point rutiranja, sada se optimizacija i definisanje matrica v vrši za svaki od parova S-D^m, gde je D^m skup destinacijskih čvorova. Međusobni uticaji u smislu minimizovanja krajnjeg rešenja dati su kroz prvi član energijske funkcije, dok se ukupna energijska funkcija dobija posle svake iteracije kao:

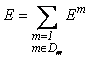
Polazeći od energijske funkcije [15], [32] i modifikujući je dodavanjem člana za optimizaciju kapaciteta, gustine i kašnjenja po linku dobija relacija 6. Vrednosti μ_{i i=1..7} su konstante kojima se pojedini članovi u jednačini 6 manje ili više ističu u odnosu na ostale, čime se utiče na priorite pojedinih uslova [33].

Prvi član jednačine (6) ima za cilj minimizaciju ukupne cene prenosa po svakoj od destinacija. Drugi član utiče da se nepostojeći linkovi eliminišu iz konačnog rešenja. Treći član obezbeđuje da tranzitni ruter koji ima ulazni link ima i odgovarajući izlazni. Četvrti ima ulogu da elementi u matrici prelaza V imaju vrednosti što bliže 0 ili 1. Peti član blokira povratnu vezu od destinacija ka izvorištu.

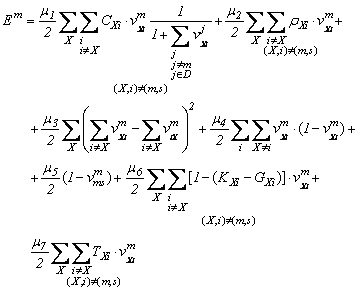(6)

Šesti je minimalan za izbor linkova kojima je preostali deo slobodnog resursa najveći, dok sedmi minimizuje kašnjenja na pojedinačnim linkovima.

Primenjujući jednačinu (5) na (6) dobija se:

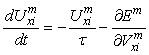
(7)

U skladu sa relacijom (1) aktivaciona funkcija je:

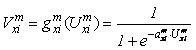(8)

4. REZULTATI SIMULACIJE

Na osnovu definisane energijske funkcije i promene stanja neurona u mreži realizovan je simulacioni model korišćenjem programskog paketa Matlab. Parametri korišćeni u simulaciji su t =1, , . Konstante μ_1-7 imaju vrednosti 600, 2500, 1500, 475, 2500, 600 i 600, respektivno. Neuroni su inicijalno pobuđeni šumom . Kraj simulacije definisan je stagnacijom energijske funkcije i maksimalnom oscilacijom u deset uzastopnih iteracija od 0,0000001. Na kraju rada programa vrednosti matrica V su zaokružene na 1 ako je ili 0 u ostalim slučajevima. U ovim primerima S=1 dok je skup D^m ={4,6,7,8}.

Polazeći od strukture mreže definisane matricama u tabelama 1-3, kreira se početna povezanost mreže i izabrana putanja u grafičkom okruženju, slika 3. Izabrana putanja je dobijena bez limitiranja maksimalno dozvoljenog kašnjenja na linkovima. Ako se ovo kašnjenje limitira na 0,9 putanja se menja i prikazana je na slici 4. Ako se ovaj uslov ograniči na 0,7 0,6 0,5 i 0,4 tada su izabrane Pareto optimalne putanje prikazane na slikama 5, 6, 7 i 8, respektivno.

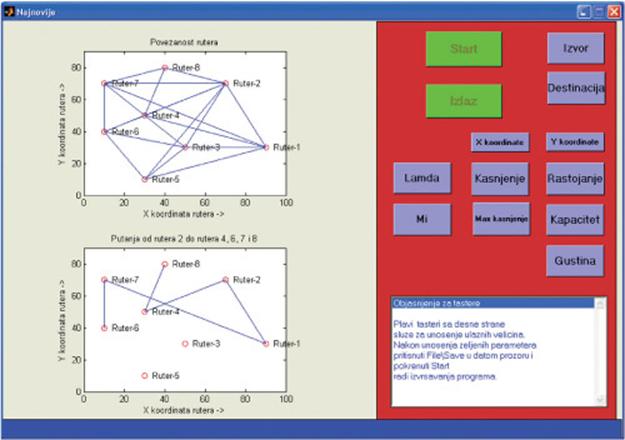
Slika 3. Početna povezanost i izabrana putanja za matrice definisane tabelama 1-3

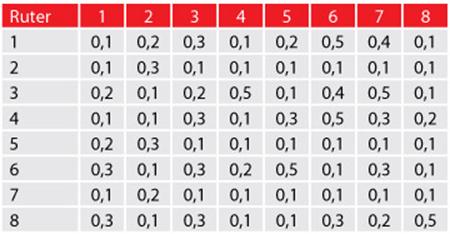
Tabela 1: Matrica cena prenosa

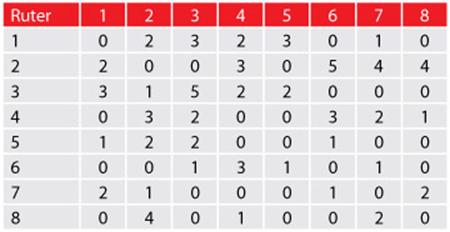
Tabela 2: Matrica kapacitet

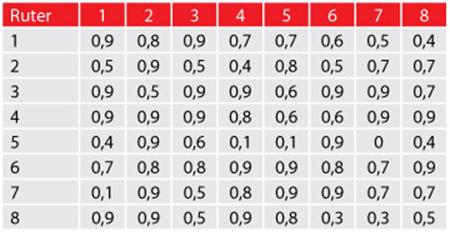
Tabela 3: Matrica gustina

Uvođenjem maksimalno dozvoljenog kašnjenja na linku, jedan broj linkova je inicijalno zabranjen, ali neki drugi će biti izbačeni od strane neuralne mreže, jer mreža tada uključuje u optimizaciju i ovaj parametar. Svaki link čija je vrednost kašnjenja bliska maksimalnoj se „loše“ odražava na njen izbor u konačnu putanju.

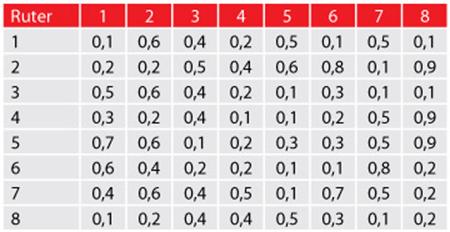
Tabela 4: Matrica kašnjenja

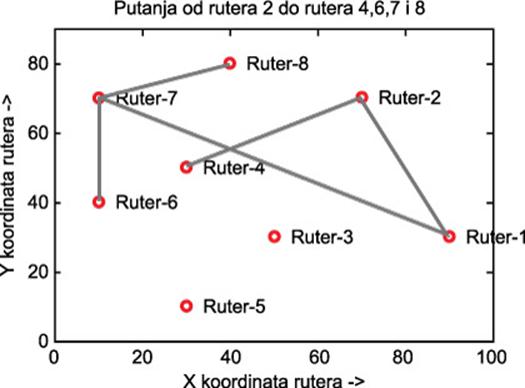
Slika 4. Izabrana putanja za parametre u tabelama 1-3 i ograničenjem maksimalnog kašnjenja na 0,9 za S=2

U slučaju linka 7-6 na slici 4, ima se vrednost kašnjenja od 0,7. Nakon povećanja kriterijuma maksimalnog kašnjenja na 0,7 ovaj link se zabranjuje i menja linkom 4-6 sa vrednošću 0,2 slika 5. Razlog zašto ovaj link i u prethodnom primeru nije bio uključen u putanju je što je razlika kapaciteta i gustine saobraćaja u prvom slučaju 0,8 a u drugom 0,1. Cena prenosa je 1 tj. 3 za drugi slučaj. Na ovaj način mreža je jedan od parametara uzela kao nepovoljniji da bi ostala tri bila višestruko bolja. Na sličan način se putanje menjaju u skladu sa daljim smanjenjem maksimalno dozvoljenog kašnjenja, a to je predstavljeno na slikama 5-8.

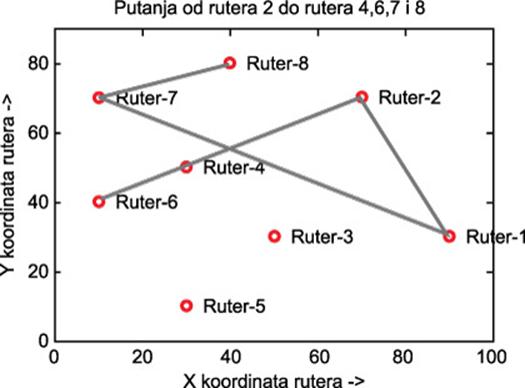
Slika 5. Izabrana putanja za parametre u tabelama 1-3 i ograničenjem maksimalnog kašnjenja na 0,7 za S=2

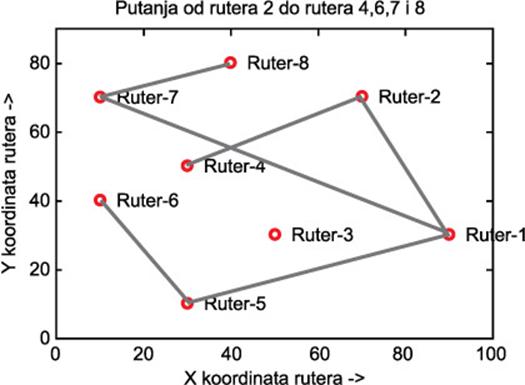
Slika. 6. Izabrana putanja za parametre u tabelama 1-3 i ograničenjem maksimalnog kašnjenja na 0,6 za S=2

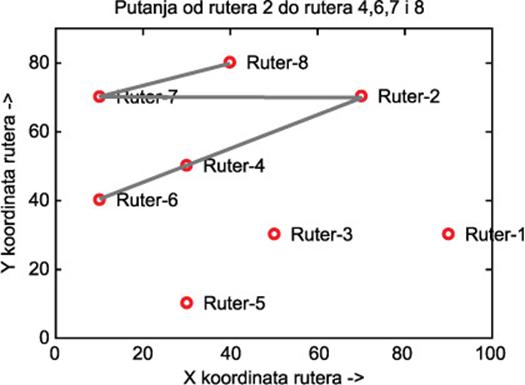
Slika 7. Izabrana putanja za parametre u tabelama 1-3 i ograničenjem maksimalnog kašnjenja na 0,5 za S=2

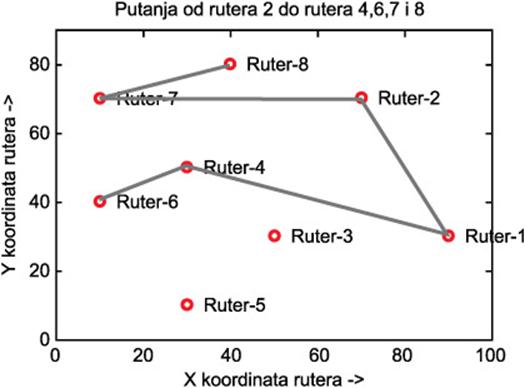
Slika 8. Izabrana putanja za parametre u tabelama 1-3 i ograničenjem maksimalnog kašnjenja na 0,4 za S=2.

Ukoliko se za podatke u tabelama 1-3 izabere S=3, i uključi maksimalno kašnjenje sa 0,9 tj. 0,7 putanje u stablu se menjaju i u potpunosti prilagođavaju kako novom izvoru, tako i kašnjenju linkova. Ovo je prikazano na slikama 9 i 10.

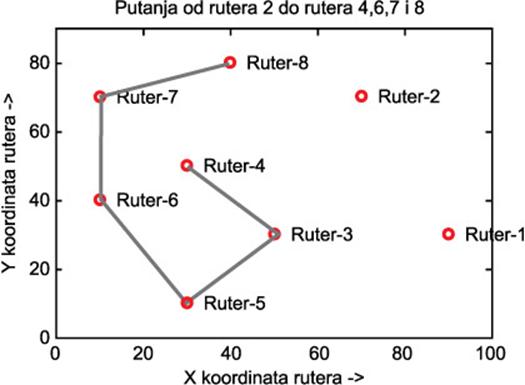
Slika 9. Izabrana putanja za parametre u tabelama 1-3 i ograničenjem maksimalnog kašnjenja na 0,9 za S=3

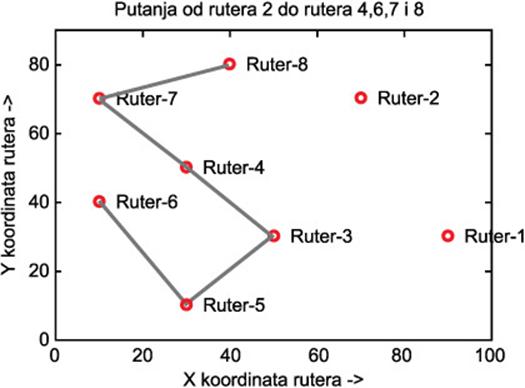
Slika 10. Izabrana putanja za parametre u tabelama 1-3 i ograničenjem maksimalnog kašnjenja na 0,7 za S=3

5. ZAKLJUČAK

U radu je opisan i razvijen model zasnovan na Hopfildovoj neuralnoj mreži za potrebe dinamičkog multicast rutiranja. Predloženi model je pokazao identične rezultate sa dostupnim u literaturi kada je reč o inicijalnim cenama linkova, ali je uveo i tri nova parametra koji u mnogome povećavaju kvalitet servisa i smanjuju verovatnoću zagušenja od prenosa video signala. Dalji rad biće usmeren na proširenje postojećeg modela i uključivanje varijacije kašnjenja u izbor konačne putanje.

Literatura

[1]M. Pioro, M. Deepankar: Routing, Flow and Capacity Design in Communication and Computer Networks, Elsevier Inc., 2004.

[2]S. Halabi, D. McPherson: Internet Routing Architectures, Cisco Press, Second edition, 2001.

[3]L. A. Giuliano, B. M. Edwards, B. R. Wright: Interdomain Multicast Routing, Addison-Wesley, 2002.

[4]D. Chakraborty, G. Chakraborty, C. Pornovalai, N. Shiratori: “Cost minimization for dynamic multicast without rerouting”, in Proc. Internet Global Summit 1999, San Jose, June 22-25, 1999.

[5]D. Chakraborty, G. Chakraborty, N. Shiratori: “”A dynamic multicast routing satisfying multiple QoS constraints”, Int. Journal of Network Management 2003; Vol. 13, 2003, pp. 321–335.

[6]T.K.Shih “Distributed Multimedia Databases: Techniques and Applications”, IGI Global, 2002.

[7]W. Jia, W. Tu, W. Zhao, G. Xu: ”Multi-shared-trees based multicast routing control protocol using anycast selection”, The International Journal of Parallel, Emergent and Distributed Systems, Vol. 20, No. 1, March 2005, pp. 69–84.

[8]I.I. Mandoiu, A. Olshevsky, A.Z. Zelikovsky: “QoS multimedia multicast routing”, Chapter 71 of Approximation Algorithms and Metaheuristics, T.E. Gonzalez, Chapman & Hall/CRC, 2007.

[9]H.Chen, B. Sun: “Multicast routing optimization algorithm with bandwidth and delay constraints based on GA”, Journal of communication and computer, Vol. 2, No.5, May 2005.

[10]R. H. Hwang, W. Y. Do, S. C. Yang: “Multicast Routing Based on Genetic Algorithms”, Journal of information science and engineering, Vol.16, 2000, pp. 885-901.

[11]Chiu D. M., S. Hurst, M. Kadansky, J. Wesley: “TRAM: A Tree-based Reliable Multicast Protocol”, Sun Microsystems Laboratories Technical Report SMLI TR-98-66, September 1998.

[12] G. Chakraborty:“Genetic Algorithm Approaches to Solve Various Steiner Tree Problems”, In Steiner Trees in Industries, Kluwer Academic, 2001, pp. 71-100.

[13] M. R. Gareg, D. S. Johnson: Computer and Intractability: A Guide to the Theory of NP-Completeness, Freeman, New York, 1979.

[14] S.L. Hakimi: “Steiner’s problem in graphs and its implications” Networks, Vol. 1, No.1, 1971, pp. 113-133

[15] C. Pornavalai, G. Chakraborty, N. Shiratori: “A neural network approach to multicast routing in real-time communication networks”, Third International Conference on Network Protocols (ICNP'95), 1995, pp. 332-339.

[16]J.Crichigno,B. Baran: “Multiobjective multicast routing algorithm” 11th International Conference on Telecommunications, Fortaleza, Brazil, August 1-6, 2004.

[17]B. Kosko: Neural networks and fuzzy systems, Prentice Hall, NJ, 1992.

[18]J. J. Hopfield, D. W Tank: “Neural computations of decision in optimization problems”, Biol. Cybern., Vol. 52, 1985, pp. 141-152.

[19]H. Rauch, T. Winarske: “Neural networks for routing communication traffic”, IEEE Cont. Syst. Mag., 1988, pp. 26-30.

[20]A. Mayer, G. Wiesbauer, M. Spitzlinger, R. Schwaiger: Applications of Hopfield networks, course project, 1999. www.cosy.sbg.ac.at

[21]B. Reljin, I. Reljin: “Rešavanje problema rutiranja pomoću neuralnih mreža”, Zbornik 13. simpozijuma o novim tehnologijama u PTT-u, Saobraćajni fakultet, Beograd, Dec. 1995.

[22]M. Ali, F. Kamoun: “Neural networks for shortest path computation and routing in computer networks”, IEEE Trans. on Neural Networks, Vol. 4, No. 6, 1993, pp. 941-953.

[23]D.C. Park, S.E. Choi: “A neural network based multi-destination routing algorithm for communication network”, Proc. Jnt. Conf. Neural Networks, Anchorage, USA, 1998, pp. 1673-1678.

[24]S. Haykin: Neural networks-a comprehensive foundation, MacMillan Collage Publishing Company, Inc., 1994.

[25]J.S. Lin, M. Liu, N.F. Huang: “The shortest-path computation in MOSPF protocol through an annealed chaotic neural network“, Proc. Natl. Sci. Counc. ROC(A) Vol. 24, No. 6, 2000, pp. 463-471.

[26]J. J. Hopfield, “Neural networks and physical systems with emergent collective computational abilities”, Proc. Nat. Acad. Sci., Vol. 79, 1982, pp. 2554-2558.

[27]J. Hopfield, D.W. Tank: “Computing with neural circuits: A model”, Science 233, 1986, pp. 625-633.

[28]V. M. N. Vo, O. Cherkaoui: “Traffic switching optimization in optical routing using Hopfield networks“, RIVF, Electronic Edition, 2004, pp. 125-130.

[29]P.D. Wasserman: Advanced methods in neural computing, Van Nostrand Reinhold, New York, 1993.

[30]C.W. Ahn, R.S. Ramakrishna, C.G. Kang, I.C. Choi: “Shortest path routing algorithm using Hopfield neural network”, Electronics Letters Vol.37, Issue 19, 2001, pp. 1176.

[31]N.Kojić, I. Reljin, B. Reljin: “Neural network for optimization of routing in communication networks”, FACTA Universitatis, Series: Electronics and Energetics, Vol. 19, No. 2, August 2006, pp. 317-329

[32]N. Kojić, I. Reljin, B. Reljin: “Optimal routing in packet switching network by using neural network”, in Proc. EUROCON-2005, Vol. 2, Belgrade, 21-24 Nov., 2005, pp. 1750-1753.

[33]N. Kojić, I. Reljin, B. Reljin: “Neural network for finding optimal path in packet-switched network” NEUREL, Beograd, Sept. 23-25, 2004.

Autori

Mr Nenad Kojić je diplomirao i magistrirao na Elektrotehničkom fakultetu u Beogradu, gde je trenutno u fazi izrade doktorske disertacije. Zaposlen je na Visokoj ICT školi, u Beogradu. Interesovanja su mu usmerena na neuralne mreže, algoritme za rutiranje, bežične mreže, obradu slike, multimediju i web tehnologije. Autor/koautor je 3 rada u časopisima i 18 konferencijskih radova. Član je grupe za Digitalnu obradu slike, telemedicinu i multimediju, na Elektrotehničkog fakulteta u Beogradu, koja je uključena u evropski projekat COST292 “Semantic Multimodal Analysis of Digital Media”. Član je domaćih društava ETRAN i Društva za telekomunikacije.

Dr Irini Reljin je diplomirala, magistrirala i doktorirala na Elektrotehničkom fakultetu u Beogradu. Zaposlena je na Visokoj ICT i Elektrotehničkom fakultetu u Beogradu. Oblast istraživanja Irini Reljin su: multimedijalni sistemi, televizija, neuralne mreže, obrada signala, optičke telekomunikacije. Iz ovih oblasti je publikovala blizu 200 naučnih i stručnih radova i nekoliko knjiga. Učestvovala je u nekoliko projekata vezanih za oblast digitalne televizije, kao i u više projekata podržanih od Ministarstva nauke. Član je grupe za Digitalnu obradu slike, telemedicinu i multimediju, na Elektrotehničkog fakulteta u Beogradu, koja je uključena u evropski projekat COST292 “Semantic Multimodal Analysis of Digital Media”. Recenzent je časopisa IEEE Communications Magazine i međunarodnih i domaćih konferencija. Član je više stručnih udruženja, međunarodnih (IEEE, SMPTE, BSUAE), i nacionalnih (ETRAN, Društvo za telekomunikacije i Udruženje jednakih mogućnosti).

Dr Branimir Reljin je diplomirao, magistrirao i doktorirao na Elektrotehničkom fakultetu u Beogradu, gde je i zaposlen. Oblast istraživanja su: obrada signala, obrada slike, veštačke neuralne mreže i njihova primena, pretraživanje velikih multimedijalnih baza, telemedicina. Ima publikovanih preko 300 radova i veći broj knjiga. Rukovodio je većim brojem međunarodnih i domaćih projekata. Član je upravnih odbora evropskih COST projekata, COST 292, “Semantic Multimodal Analysis of Digital Media”, i COST IC 0604, “Anatomic Telepathology Network (EURO-TELEPATH)”, i član je COST komiteta za oblast ICT. Član je više međunarodnih i nacionalnih stručnih i profesionalnih udruženja (IEEE Senior Member). Predsednik je simpozijuma o veštačkim neuralnim mrežama, NEUREL, koji je podržan od udruženja IEEE. Recenzent je više međunarodnih časopisa i konferencija.