Srpski / Aktuelni broj / BOJANA ANĐELIĆ: Problem rutiranja i dodjele talasnih dužina u optičkim WDM mrežama
PROBLEM RUTIRANJA I DODJELE TALASNIH DUŽINA U OPTIČKIM WDM MREŽAMA
Bojana Anđelić, Rеpublička agencija za elektronske komunikacije (RATEL)*
SADRŽAJ
U ovom radu se razmatraju problem rutiranja i dodjele talasnih dužina (routing and wavelenght assignment, RWA) u optičkim mrežama baziranim na multipleksiranju talasnih dužina (Wavelength Division Multiplexing, WDM) i klasifikacija problema i algoritama RWA. Biće riječi i o metaheuristikama za rješavanje ovog problema, sa akcentom na dvije, a to su Tabu pretraživanje (Tabu search, TS) i Metoda promjenljivih okolina (Variable neighbourhood search, VNS).
Ključne reči: algoritam RWA, heuristike, tabu pretraživanje, metoda promjenljivih okolina
Bojana Anđelić, Rеpublic Agency for electronic communications (RATEL)*
ABSTRACT
This paper takes into consideration the problem of routing and wavelenght assignment (RWA) in optical networks based on wavelength division multiplexing (WDM) and the classification of RWA problems and algorithms. Metaheuristics for solving this problem will also be considered, and especially two of them, the tabu search (TS) and the variable neighbourhood search (VNS).
Keywords: RWA algorithm, heuristics, tabu search, variable neighbourhood search
1. UVOD
Mreža WDM se sastoji iz čvorova koji su međusobno povezani optičkim vlaknima preko kojih se prenose signali po talasnim dužinama. Signal pri prolasku kroz čvorove optičke mreže može da bude prethodno obrađen u elektronskom formatu, što nije uvijek slučaj. Budućnost ovih mreža jesu potpuno optičke mreže (all optical networks) u kojima se svetlosne putanje od izvorišta do odredišta u potpunosti realizuju u optičkom domenu. Trenutni tehnološki razvoj još uvijek ne omogućava upotrebu ovih mreža, jer se javlja veliki broj problema pri implementaciji [1]. Predložene su translucentne mreže. U translucentnoj mreži samo pojedini unaprijed odabrani čvorovi imaju mogućnost obrade signala u električnom domenu.
Postoje 4 tipa čvorova u odnosu na mogućnost promjene talasnih dužina, i to: bez konverzije, sa ograničenom konverzijom, sa fiksnom konverzijom i sa potpunom konverzijom talasnih dužina [2]. Za veću iskorišćenost linkova najbolji su optički čvorovi sa potpunom konverzijom. Veoma je velika razlika između cijena ovih tipova čvorova, stoga treba napraviti neki vid kompromisa između iskorišćenosti linkova i zahtjeva u pogledu saobraćaja na jednoj strani i budžeta predviđenog za realizaciju mreže na drugoj.
Problem pronalaska optimalne svjetlosne putanje u optičkoj mreži WDM se rješava algoritmom za rutiranje i dodjelu talasnih dužina. Veoma je važno razviti brz i efikasan algoritam rutiranja i dodjele talasnih dužina (RWA) koji će biti implementiran. Algoritmi se zasnivaju na primjeni različitih egzaktnih, aproksimativnih i heurističkih/metaheurističkih metoda.
2. KLASIFIKACIJA PROBLEMA I ALGORITAMA RUTIRANJA I DODJELE TALASNIH DUŽINA (RWA)
Problem RWA u mrežama WDM je razdvojen na dva nezavisna potproblema, a to su rutiranje i dodjela talasnih dužina.[3] Algoritam rutiranja podrazumijeva pronalazak slobodnih putanja, a algoritam dodjele talasnih dužina zauzimanje slobodnih talasnih dužina na linkovima duž tih putanja.
Ograničenja koja se postavljaju pri rješavanju problema RWA se odnose na to da dvije putanje sa istim talasnim dužinama ne mogu biti rutirane preko istog fizičkog linka. Ovo ograničenje se zove ograničenje konfliktnosti ili različitosti talasnih dužina. Drugo ograničenje koje mora biti zadovoljeno u mrežama bez konverzije talasnih dužina se odnosi na to da jednoj putanji mora biti dodjeljena ista talasna dužina na svim fizičkim linkovima duž izabrane rute. Ono se naziva ograničenje kontinuiteta talasne dužine.
Prema scenariju saobraćaja problemi RWA se mogu podijeliti u dvije opšte kategorije[4]: statičke (static lightpath establishment, SLE) i dinamičke (dynamic lightpath establishment, DLE). Klasifikacija saobraćaja je prikazana na Slici 1. [5] gdje SLDs (Sheduled Lightpath Demand) predstavljaju zahtjeve za konekcije, pri čemu su unaprijed određeni izvori, odredišta, broj konekcija, kao i vrijeme uspostavljanja i raskida istih. U slučaju statičkog scenarija matrica zahtjeva za konekcije (putanja koje želimo da uspostavimo) je unaprijed poznata, pri čemu je neophodno uspostaviti u mreži sve konekcije odjednom. Svaka konekcija ima neograničeno vremensko trajanje. Ovi problemi se izvršavaju u režimu oflajn. U zavisnosti od kriterijumske funkcije ovi problemi RWA mogu biti problemi Min-RWA ili Max-RWA. Kad je problem RWA minimiziranje potrebnog broja talasnih dužina tako da sve zahtjevane konekcije budu uspostavljene, onda se radi oproblemu Min-RWA. Ako se rješava dualni zadatak kojim se za unaprijed dati broj raspoloživih talasnih dužina maksimizira broj uspostavljenih konekcija u mreži onda je reč o problemu Max-RWA.
Kod dinamičkog problema RWA, zahtjevi za konekciju između pojedinih čvorova u mreži se uspostavljaju potpuno slučajno u vremenu i imaju slučajno vremensko trajanje. Ovi problemi se izvršavaju u režimu onlajn. Odluke o izboru putanje moraju da se donose u realnom vremenu, u momentu nailaska pojedinačnog zahtjeva, stoga dinamičko rutiranje koristi informacije o trenutnom stanju o zauzetosti mreže. Ovaj problem je kompleksan za rješavanja posebno kada su u pitanju veće mreže. Iz tog razloga se problem RWA razdvaja na dva gore pomenuta nezavisna potproblema.
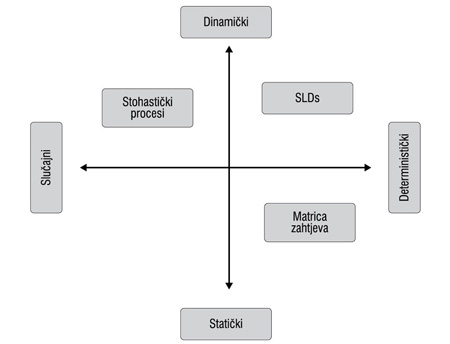
Slika 1. - Klasifikacija saobraćaja.
2.1 Potproblem rutiranja
Jedan od problema u implementaciji optičkih mreža se odnosi naparametar kvaliteta servisa u mreži, a to je vjerovatnoća blokade. Naime kada je opterećenje u mreži veliko broj blokiranih konekcija značajno raste. U praksi se pokazalo da su određeni linkovi znatno više opterećeni od drugih i da se blokada javlja usled zagušenja na njima. Da bi se izvršila prevencija ovog slučaja neophodno je da se pronađu alternativne putanje kojima će se preneti signali, i time smanjiti vjerovatnoća blokade.
Algoritmi rutiranja se mogu podijeliti u zavisnosti od toga da li postoje ograničenja u pogledu broja potencijalnih putanja na: fiksno rutiranje (Fixed Routing, FR), alterativno rutiranje (Alternative Routing, AR) i iscrpljujuće rutiranje (Exhaust Routing, ER). Ovi algoritmi su nešto detaljnije objašnjeni u [6].
Algoritam fiksnog rutiranja je najjednostavniji metod rutiranja jer se za svaki par čvorova unaprijed odredi samo jedna fiksna ruta koja je po pravilu najkraća između datih čvorova, a dobijena pomoću algoritama kao što su Dajkstrin ili Belman-Fordov algoritam. Fiksno rutiranje ne može da prevaziđe situacije kao što je pad linka.
Algoritmom alternativnog rutiranja za svaki par čvorova odredi se unaprijed skup od k mogućih ruta kandidata koji predstavlja podskup svih mogućih ruta za dati par čvorova. Izbor raspoložive rute za uspostavljanje konekcije može se vršiti prema fiksnom redoslijedu (Fixed Alternate Routing, FAR) ili adaptivno izborom rute sa najvišim brojem slobodnih talasnih dužina na ruti (Least Congestion Routing, LCR). Algoritam LCR na pojavu zahtjeva za uspostavljanje konekcije pretražuje skup ruta kandidata proračunavajući za svaku od njih cijenu koja se određuje na osnovu stepena zagušenosti rute. Mana algoritma LCR je u složenosti računanja tih cijena. Algoritam alternativnog rutiranja omogućava jednostavnost kontrole uspostave i raskida konekcija, a takođe njime može da se postigne i određeni stepen tolerancije na otkaze linkova. Prednost u odnosu na algoritam fiksnog rutiranja bi bila mogućnost značajnog smanjenja vjerovatnoće blokiranja čak i kad je u pitanju postojanje samo dvije alternativne putanje.
Algoritam ER bira rutu za uspostavljanje konekcije između datog para čvorova iz skupa svih mogućih ruta bez ograničenja. Ovaj algoritam koristi informacije o stanju mreže u formi grafa. Mana ovog algoritma je relativno velika kompleksnost i dužina vremena potrebna za izbor preferentne rute i pripadajuće talasne dužine.
Ovi navedeni algoritmi nezavisno prvo biraju rutu pa zatim vrše izbor talasne dužine. Može i obrnutim redoslijedom. Takođe, moguće je primijeniti i algoritme sa istovremenim izborom talasne dužine i rute (joint wavelength-route selection, JWR). Algoritam JWR za svaki par čvorova unaprijed odredi skup ruta kandidata kao podskup svih mogućih ruta za dati par.
2.2 Potproblem dodele talasnih dužina
Najjednostavnija klasifikacija algoritama za izbor talasne dužine može se izvršiti prema redoslijedu po kome se traži slobodna talasna dužina za konekciju. Pomoću heuristika, talasna dužina može biti izabrana: slučajnim redoslijedom (random, R), po fiksnom redoslijedu (first-fit, FF), kao najmanje korišćena (least-used, LU), kao najviše korišćena (most-used, MU), i na neke druge načine koje ćemo samo nabrojati: Min-Product, Least Loaded, MAX-SUM, Relative Capacity Loss, Distributed Relative Capacity Loss, Wavelength Reservation i Protecting Treshold.[4]
Redoslijed pretraživanja talasnih dužina u algoritmu R je slučajan, a preferentna je prva slobodna na koju se naiđe iz skupa svih talasnih dužina.
Algoritam FF pretražuje talasne dužine po unaprijed utvrđenom fiksnom redoslijedu, a preferentna za uspostavljanje veze je prva slobodna na koju se naiđe.
U algoritmu LU preferentna je ona talasna dužina koja se koristi na najmanjem broju linkova u mreži, tj. pretraživanje se vrši po rastućem nizu. Performanse su lošije nego kad se primjenjuje algoritam R, dok pri LU još prethodno mora da se izračuna koja talasna dužina se koristi na najmanjem broju linkova.
Algoritam u kome se talasna dužina bira po kriterijumu najviše korišćene (MU) pretražuje skup talasnih dužina po opadajućem redoslijedu u odnosu na broj linkova na kojima se svaka od njih koristi, što znači suprotno od algoritma LU. Vrijeme potrebno za računanje je kao kod algoritma LU, ali ovaj algoritam za razliku od algoritma LU daje nešto bolje rezultate od algoritma FF.
3. METAHEURISTIKE ZA RJEŠAVANJE PROBLEMA RWA
Pri rješavanju statičkih i dinamičkih problema RWA mogu se primijeniti dva pristupa. Kao što je već pomenuto, prvi je integralno rješavanje problema RWA, dok drugi podrazumijeva dekompoziciju problema RWA na dva sastavna potproblema, potproblem rutiranja i potproblem dodjele talasnih dužina, koji se nezavisno rješavaju proizvoljnim redoslijedom. Performanse koje se postižu primijenom pojedinih algoritama zavise od primjenjenog načina i redoslijeda rešavanja potproblema. Potrebno je naglasiti da nema univerzalno dobrog algoritma već se koriste algoritmi u zavisnosti od pojedinačnog problema.
Prema definiciji, klasa problema odlučivanja koji se mogu riješiti u polinomijalnom vremenu pomoću nedeterminističkog algoritma označava se sa NP (nedeterministički polinomijalni).[7] Problem koji pripada ovoj klasi se naziva NP-problem. Takođe prema definiciji, NP-problem se naziva NP-potpun ako za svođenje bilo kojeg NP-problema na posmatrani problem postoji polinomijalni algoritam, tj. ako se bilo koji NP-problem polinomijalno transformiše u posmatrani problem. Problem koji nije problem odlučivanja, a čije rešavanje nije jednostavnije od rešavanja nekog NP-potpunog problema, naziva se NP-težak.
Poznati algoritmi za rješavanje NP-teških problema su u najboljem slučaju eksponencijalne složenosti. Pojednostavljeno, kombinatorna optimizacija je matematička disciplina koja proučava probleme nalaženja ekstremnih vrijednosti funkcije definisane na konačnom skupu. U oblasti kombinatorne optimizacije nailazi se na probleme čije rješavanje uz pomoć algoritama nije adekvatno zbog velikog utroška računarskog vremena. Zbog toga se odustaje od algoritama za (tačno) rješavanje problema i pribjegava heuristikama. Heuristike ne garantuju nalaženje rјešenja problema, ali dobre heuristike rјešavaju problem u velikom broju slučajeva. Kod optimizacionih problema algoritam nalazi optimalno rјešenje, a heuristike daju suboptimalna rјešenja. Dobre heuristike daju suboptimalna rјešenja koja su bliska optimalnom rјešenju.[7]
Jedan od matematičkih alata koji se koristi za rješavanje problema linearne optimizacije (Linear Programming, LP) radi dobijanja tačnih rezultata je CPLEX. Pomoću njega može da se riješi i nekoliko ekstenzija LP problema, kao što su: problemi protoka kroz mrežu, problemi kvadratnog programiranja (Quadratic Programming, QP), problemi QCP (Quadratically Constrained Programming), problemi MIP (Mixed Integer Programming). Međutim, CPLEX nailazi na probleme kada je velika kompleksnost (veliki broj čvorova i/ili talasnih dužina u mreži) u pitanju. Rјešavanje pomoću njega nije adekvatno zbog velikog utroška računarskog vremena i memorije koju koristi.
Tokom posljednje dvije decenije se počelo sa razvojem tzv. „metaheurističkih algoritama“. Oni predstavljaju opšte heurističke algoritme za rješavanje problema kombinatorne optimizacije, a slobodniji prevod bi glasio algoritmi „visokog nivoa“. Drugim riječima, metaheuristički algoritmi su heuristički algoritmi visokog nivoa koji se koriste za rješavanje složenih problema kombinatorne optimizacije za koje ne postoje odgovarajući heuristički algoritmi. Metaheuristički algoritmi predstavljaju strategije pretraživanja najvišeg ranga koje usmeravaju i vode ostale heurističke algoritme prilikom pretraživanja prostora dopustivih rješenja.[8]
U najpoznatije metaheuristike spadaju Simulirano kaljenje, Genetski algoritmi, Tabu pretraživanje, Metoda promjenljivih okolina, Optimizacija kolonijom mrava i Optimizacija kolonijom čestica.
Biće riječi o Tabu pretraživanju i Metodi promjenljivih okolina. Uopšteno govoreći, obje metaheristike se sastoje iz tri faze: pripremne faze, određivanja inicijalnog rješenja (početnog rješenja) i popravljanja istog.
3.1 Tabu pretraživanje
Osnovni koncept tabu pretraživanja kao heurističke metodologije za rješavanje problema RWA predložio je Glover 1986. godine, dok su slične ideje nezavisno razvili Hansen i Žomar 1987. godine.[9]
Tabu pretraživanje se zasniva na principu lokalnog pretraživanja. Glavni nedostatak lokalnog pretraživanja je to što se pretraživanje može „zaglaviti“ u okolini lokalnog minimuma. Kod Tabu pretraživanja ovaj nedostatak je prevaziđen tako što ova heuristika pored korišćenja lokalnog minimuma, dozvoljava i „uzlazne“ pomake na strogo kontrolisan način, tj. pomake koji „vode“ u susјede sa lošijom vrijednošću funkcije cilja.
Najvažnija komponenta tabu pretraživanja je tzv. adaptivna memorija, pamćenje nekih podataka o prethodnih fazama procesa pretraživanja, koje zatim utiču na izbor sledećih tačaka u ovom procesu. U svakoj iteraciji n čuva se neka istorija H prethodnog pretraživanja, tj. pamte se izabrane karakteristike nekih od prethodno generisanih tačaka. U osnovnoj verziji TP se koristi samo jedan tip adaptivne memorije, a to je tzv. kratkotrajna memorija (recency-based memory). Osim pomenute kratkotrajne predložena je i dugotrajna memorija (frequency-based memory).[10] Postojanje kratkotrajne i dugotrajne memorije omogućava diversifikaciju i intensifikaciju pretrage za najboljim rješenjem problema kombinatorne optimizacije. Diversifikacija procesa pretraživanja podrazumijeva istraživanje što većeg broja različitih regiona u prostoru dopustivih rješenja.
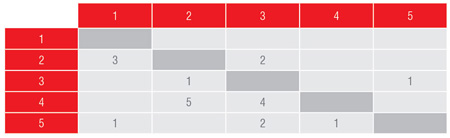
Radi pojašnjena koristimo primjer iz [8] sa matricom u Tabeli 1. koja ilustruje koncept kratkotrajne i dugotrajne memorije. Pretpostavka je da je već izvršeno 17 iteracija. Takođe, pretpostavimo da svaka izvršena zamjena ima tabu status tokom naredne dvije iteracije. Kratkotrajnoj memoriji pripadaju ćelije iznad, a dugotrajnoj ispod glavne dijagonale. Vidimo iz Tabele 1. poslednje dvije izvršene zamjene, zamjena (2,3) i zamjena (3,5). Takođe, ispod glavne dijagonale vidimo vrijednost učestanosti koja ukazuje koliko puta je od početka procesa pretraživanja izvršena određena zamjena.
Tabela 1. - Kratkotrajna i dugotrajna memorija.
Diversifikacija procesa pretraživanja podrazumijeva istraživanje što većeg broja različitih regiona u prostoru dopustivih rješenja. Postiže se penalizovanjem zamjena kojima odgovara velika vrijednost učestanosti. Neka je pet najboljih zamjena prikazano u Tabeli 2. Zamene (3,5) i (2,3) bi dovele do smanjivanja vrijednosti kriterijumske funkcije, međutim one imaju tabu status. Ostale zamjene ne mogu da dovedu do smanjivanja vrijednosti kriterijumske funkcije jer je njihova ušteda negativna.
Tabela 2. – Najboljih pet zamjena.
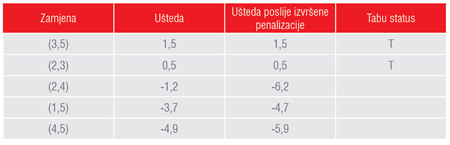
Prema Tabeli 2. zamjena koja bi donijela najmanju negativnu vrijednost uštede je zamjena (2,4). Pri tome treba uzeti u obzir i vrijednosti učestanosti iz dugotrajne memorije. Neka penalizacija određene zamjene uzme vrijednost učestanosti zamjene. Posle izvršene penalizacije imamo nove vrijednosti uštede koje su takođe prikazane u Tabeli 2. Zaključak je da treba izvršiti zamjenu (1,5) pri čemu nam je penalizacija omogućila da posetimo manje poznati region u prostoru dopustivih rješenja.
Efikasnost primjene Tabu pretraživanja zavisi od sljedećeg:
- načina generisanja početnog rešenja,
- definicije okoline,
- izbora atributa koji će se pamtiti u tabu listama,
- dužine tabu lista,
- izbora kriterijuma aspiracije,
- načina dobijanja potskupa
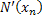 , itd.
, itd.
3.2 Metoda promjenljivih okolina
Ova metoda je prvi put predstavljena 1995. godine u radu N. Mladenovića [11]. Podrazumijeva sistematičnu promjenu okoline sa algoritmom lokalnog pretraživanja što vodi ka jednostavnijoj i efikasnijoj metaheuristici za rješavanje problema kombinatorne optimizacije. Promjena okoline može biti i „drastična“, tj. iz jedne okoline se može preći u drugu koja je njoj daleka.
Postoje unaprijed definisane strukture okoline sa ![]() , kao i
, kao i ![]() , skup rješenja u k-toj okolini tačke x. Ova metoda se zasniva na sljedećim postulatima:
, skup rješenja u k-toj okolini tačke x. Ova metoda se zasniva na sljedećim postulatima:
- Lokalni minimum u okviru jedne strukture okoline nije nužno/obavezno i lokalni minimum u drugoj strukturi okoline.
- Globalni minimum mora biti i lokalni minimum za sve strukture okoline.
- Pri rješavanju mnogih problema lokalni minimumi jedne ili više okolina su relativno bliski jedan drugom.
U cilju dobijanja što boljih rezultata uz pomoć Metode promjenljivih okolina mora se voditi računa o sljedećem:
- broju i vrsti struktura okolina koja se koristi,
- redoslijedu po kojem se vrši pretraživanje,
- strategiji promjene okoline,
- metodi koja se koristi za lokalno pretraživanje,
- kriterijumima zaustavljanja.
Osnovni algoritam Metode promjenljivih okolina kombinuje deterministički i stohastički pristup promjeni okoline [12]. Nalazimo se u prvoj okolini tačke ![]() . Tačka
. Tačka ![]() predstavlja početno rješenje. Sljedeća faza počinje sa funkcijom koja se zove razmrdavanje (Shake). Ona podrazumijeva generisanje rješenja na slučajan način u odnosu na početno rješenje (tj. generisanje tačke
predstavlja početno rješenje. Sljedeća faza počinje sa funkcijom koja se zove razmrdavanje (Shake). Ona podrazumijeva generisanje rješenja na slučajan način u odnosu na početno rješenje (tj. generisanje tačke ![]() na slučajan način iz k-te okoline tačke
na slučajan način iz k-te okoline tačke ![]() (
(![]() da bi se izbjeglo ponovno vraćanje u istu tačku (cycling). K predstavlja broj realizovanih putanja koje će se osloboditi i potom pokušati realizovati putanje koje prethodno nisu bile realizovane. Na taj način se formiraju rješenja koja čine okolinu tačke
da bi se izbjeglo ponovno vraćanje u istu tačku (cycling). K predstavlja broj realizovanih putanja koje će se osloboditi i potom pokušati realizovati putanje koje prethodno nisu bile realizovane. Na taj način se formiraju rješenja koja čine okolinu tačke ![]() . Za slučaj prve okoline znači da će se osloboditi jedna realizovana putanja. Zatim slijedi lokalno pretraživanje i to sa strategijom prve popravke (First Improvement), koja se zaustavlja kad se dobije prvo bolje rješenje
. Za slučaj prve okoline znači da će se osloboditi jedna realizovana putanja. Zatim slijedi lokalno pretraživanje i to sa strategijom prve popravke (First Improvement), koja se zaustavlja kad se dobije prvo bolje rješenje![]() od prethodno slučajno generisanog rješenja
od prethodno slučajno generisanog rješenja![]() . Pod boljim rješenjem se u našem slučaju podrazumijeva povećanje broja razrješenih zahtjeva. Ova strategija se koristi iz razloga da se ne bi trošilo suviše mnogo vremena kao što bi ako bi se pretraživala čitava okolina tačke
. Pod boljim rješenjem se u našem slučaju podrazumijeva povećanje broja razrješenih zahtjeva. Ova strategija se koristi iz razloga da se ne bi trošilo suviše mnogo vremena kao što bi ako bi se pretraživala čitava okolina tačke ![]() . Samo u krajnjem slučaju se pretražuje čitava okolina tačke
. Samo u krajnjem slučaju se pretražuje čitava okolina tačke ![]() , tj. ako se ne naiđe ni na jedno poboljšanje, ili se pretraga zaustavlja ako istekne unaprijed određeno vrijeme.
, tj. ako se ne naiđe ni na jedno poboljšanje, ili se pretraga zaustavlja ako istekne unaprijed određeno vrijeme.
Znamo da lokalni minimum jedne okoline ne mora biti i lokalni minimum druge okoline. Stoga, postoji lokalno pretraživanje koje se zove Metoda spusta kroz promjenljive okoline (Variable neighbourhood descent, VND).[12] Ovom metodom je moguće promijeniti okolinu i tokom lokalnog pretraživanja. Pronalazi se najbolje rješenje u svakoj okolini. Većina heuristika koje se koriste za lokalno pretraživanje u fazi spuštanja koristi mali broj okolina, najčešće jednu ili dvije. Šanse da se dosegne globalni minimum sa VND su veće nego kad se koristi samo jedna struktura okoline. Osim toga, korišćenjem sekvencijalnog poretka struktura okolina u VND-u, može da se razvije i ugnježdena strategija. Neka je ![]() . Moguća ugnježdena strategija bi podrazumijevala da se izvrši VND na prve dvije okoline, za svaku tačku
. Moguća ugnježdena strategija bi podrazumijevala da se izvrši VND na prve dvije okoline, za svaku tačku ![]() koja pripada trećoj okolini (
koja pripada trećoj okolini (![]() . Ovaj pristup je prisutan u [13].
. Ovaj pristup je prisutan u [13].
Redukovana metoda promjenljivih okolina (Reduced VNS, RVNS) se koristi kad lokalno pretraživanje traje jako dugo, zbog čega se ono i izbacuje iz metode. Odmah nakon razmrdavanja se proverava da li je dobijeno bolje rješenje da bi se odmah promijenila okolina. Postoje dva parametra, ![]() i
i ![]() . Parametar
. Parametar ![]() može, između ostalog, da predstavlja maksimalno dozvoljeno vrijeme računanja ili maksimalan broj iteracija koji može da se izvrši između dva poboljšanja. Uz pomoć „razmrdavanja“ generišemo na slučajan način tačku
može, između ostalog, da predstavlja maksimalno dozvoljeno vrijeme računanja ili maksimalan broj iteracija koji može da se izvrši između dva poboljšanja. Uz pomoć „razmrdavanja“ generišemo na slučajan način tačku ![]() u k-toj okolini tačke
u k-toj okolini tačke ![]() , tj.
, tj. ![]() . Ustanovljeno je da se najbolja vrijednost često dobija za
. Ustanovljeno je da se najbolja vrijednost često dobija za ![]() . Ova metoda je slična metodi Monte-Karlo, pri čemu je sistematičnija. RVNS se ograničava na neku okolinu dok metoda Monte-Karlo izbegava sistematsko pretraživanje i bira rješenje u cijelom prostoru dopustivih rješenja.
. Ova metoda je slična metodi Monte-Karlo, pri čemu je sistematičnija. RVNS se ograničava na neku okolinu dok metoda Monte-Karlo izbegava sistematsko pretraživanje i bira rješenje u cijelom prostoru dopustivih rješenja.
Metoda promjenljivih okolina sa dekompozicijom (Variable Neighbourhood Decomposition Search, VNDS) predstavlja proširenje metode VNS i to tako da se problem raščlanjuje na potprobleme. Uvodi se i dodatni parametar ![]() koji predstavlja vremensko ograničenje za potprobleme.
koji predstavlja vremensko ograničenje za potprobleme.
Kod Adaptivne metode promjenljivih okolina (Skewed VNS, SVNS), za kriterijum prelaska iz jednog lokalnog minimuma u drugi se, pored vrijednosti funkcije cilja, uzima i udaljenost između tih lokalnih minimuma.
4. ZAKLJUČAK
Predstavljeni su mnogi algoritmi rutiranja i dodjele talasnih dužina u optičkim mrežama WDM, kao i dvije metaheuristike, TS i VNS i njene varijante, za rјešavanje problema RWA. U slučaju velike kompleksnosti mreže, za rješavanje problema RWA neophodna je primjena efikasne heuristike. Generalno, upotreba TS i VNS se pokazala veoma uspješnom pri rjеšavanju problema RWA. Stoga bi se mogle primjeniti varijante VNS pri rješavanju problema RWA radi utvrđivanja kad je koja varijanta pogodnija da se koristi. Potrebno je shvatiti značaj primjene metaheuristika u problematici projektovanja i eksploatacije optičkih telekomunikacionih mreža.
Literatura
[1] Gangxiang Shen and Rodney S. Tucker: “Translucent Optical Networks: The Way Forward”, IEEE Communications Magazine, Vol. 45, No. 2, February 2007, pp. 48-54.
[2] D. Medhi and K. Ramasamy: Network Routing: Algorithms, Protocols, and Architectures, Morgan Kaufmann, San Francisco, 2007.
[3] V. Tintor: “Algoritmi rutiranja u translucentnim optičkim mrežama”, TELFOR 2009, 2009. godine.
[4] B. Mukherjee: Optical WDM Networks, Springer, New York, 2006.
[5] “Optimization Problems in WDM Optical Transport Networks with Scheduled Lightpath Demands”, Ph. D. Thesis of Josu_e Kuri, September 12, 2003.
[6] Goran Z. Marković, Vladanka S. Aćimović-Raspopović: “Optimizacija korišćenja resursa u optičkim WDM mrežama primenom RWA algoritama”, 15. Telekomunikacioni forum TELFOR, Srbija, Beograd, 2007.
[7] D. Cvetković, M. Čangalović, Đ. Dugošija, V. Kovačević-Vujičić, S. Simić, J. Vuleta: Kombinatorna optimizacija, Matematička teorija i algoritmi, Društvo operativnih istraživača Jugoslavije, Beograd, 1996.
[8] D. Teodorović: Transportne mreže, Univerzitet u Beogradu, Beograd, 1996.
[9] P. Hansen, B. Jaumard: “Algortihms for the maximum satisfability problem”, RUTCOR Research Report RR43-87, Rutgers University, New Brunswick, New Jersey, 1987.
[10] F. Glover, M. Laguna: Tabu Search, Kluwer Academic Publishers, Boston, 1997.
[11] N. Mladenović: „A variable neighborhood algorithm – a new metaheuristic for combinatorial optimization applications“, Presented at Optimization Days, Montreal, 1995.
[12] P. Hansen, N. Mladenović, J.A. Moreno Pérez: “Variable neighborhood search: methods and applications”, 4OR: A Quarterly Journal of Operations Research, Volume 6, Number 4, December 2008, pp. 319-360.
[13] P. Hansen, N. Mladenović: „Variable neighborhood search: Principles and applications“, European Journal of Operational Research 130, 2001, pp. 449-467.
Autor
Bojana Anđelić je diplomirala (2008) i stekla titulu mastera (2010) na Katedri za telekomunikacije Elektrotehničkog fakulteta Univerziteta u Beogradu, na kome trenutno pohađa doktorske studije. Zaposlena je u Republičkoj agenciji za elektronske komunikacije. Do sad je objavila jedan rad sa grupom autora u časopisu IET Communications.