CASOPIS REPUBLICKE AGENCIJE ZA TELEKOMUNIKACIJE

Abstract. In transmission of laser beam through lossless space or through lenses or non-uniform media, the beam parameters change. If paraxial approximation is applicable, many problems in beam propagation through various media conditions can be reduced to closed form solutions. In this paper we consider transformation of circular and elliptical laser beam of Gaussian shape in passing through uniform medium or through lens or system of lenses.

Key words: Laser circular and elliptical beams, lenses, beam parameters.

Basic geometry used in calculation of circular laser beam is shown In Fig.1. In the aperture we assume the scalar field of the form

(1)

where is the axial field intensity at , and is the beam waist.

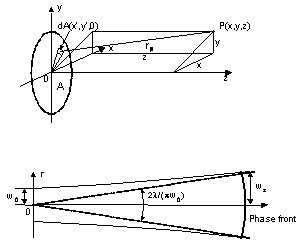
Fig.1. Geometry used in defining laser beam

Analytical expression for the beam at the plane, can be expressed in the form

(2)

where the beam radius and the radius of the phase front at are

, ,

with , , is the wavelength. At distances for which,

, and.

The far field is again Gaussian but with the complex parameters

(3)

For a given laser and are constants. If we take into account that we see that the far field beam is again circular and there is noangle dependence. The axial field amplitude decreases inversely with the distance. At a fixed distance, the contours of constant amplitude and phase are circles.

The transformation of Gaussian beam through a converging or diverging lens can be obtained by simple calculations based on the q parameter binomial transformation [3]. However, if the lens radius is comparable with the beam radius significant errors are encountered and we need to solve a complex electromagnetic problem. Here we will show steps to be taken if the lens radius is arbitrary.

(4)

For the sake of simplicity we can now assume to have a lens of infinite size so that the aperture field behind the lens can be expressed as the Kirchhoff's-Huygens integral. If the size of lens is finite then the integral limits have to be reduced and no closed form solution is possible.

(5)

where and . In the expression for new axial coordinate is measured from the aperture to the observation point behind the lens. In this approximation we can put in the denominator.

The integral (5) can be converted in the form suitable for integration. After some manipulations we reduce problem to solving the integral (shown only for the variable x’)

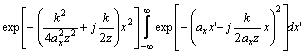(6)

where

After substitution , the integral in Eq.(6) can be solved and the final result is

(7)

In a similar way the integral with respect to y' leads to

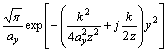(8)

The electromagnetic field radiated from an aperture illuminated by the field:

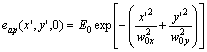(9)

where are the waists of the Gaussian elliptical beam and is the electric field on the beam axis. The radiated field at some distance z=z₁ can be written in the form [5]:

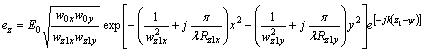
(10)

(11)

For the sake of simplicity we can now assume to have a lens of infinite size so that the aperture field behind the lens can be expressed as:

(12)

where again we used as the aperture coordinates, but they are different from those used in Eq. (9).

To find the radiation field we apply the Kirchhoff's-Huygens integral

(13)

where . Notice that the coordinate z is measured from the lens aperture so that we do not take into account the distance between the waists plane and the lens plane z₁.

Calculation of the double integral in (13) can be simplified if we assume that in the denominator can be replaced by z, and in the exponential term by

(14)

Now the radiation field can be calculated from two line integrals as the integrand in this case can be written in the form of product of functions , where

(15)

(16)

We can convert the above expressions in the form suitable for integration. After some manipulations that lead to the integral (shown only for the x' )

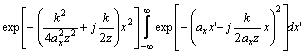(17)

where

After substitution , the integral in Eq.(17) can be solved and the final results is

(18)

In a similar way the integral with respect to y' leads to

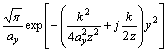(19)

where

Finally

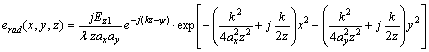(20)

The radiated field is also Gaussian and the 1/e half width at some distance z can be found after separating the real part of the term

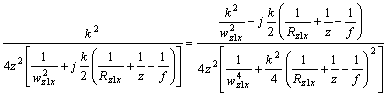(21)

The required square of the 1/e half-widths are then

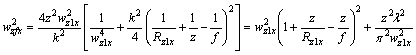(22)

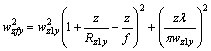(23)

For z=0 we have and as it should be. The position of the beam waist after the lens is obtained from the derivative of (22) or (23). For the x-component it is

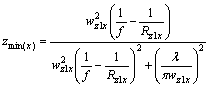(24)

After substitution of w_z1x and R_z1x from Ref.[5] into Eq.(24), identical expression as the one obtained by the q-parameter calculation is found:

For the y-component similar calculation leads to

(26)

Upon substitution of the beam waist position from Eq.(24) into Eq.(22) it is found that the waist is

(27)

for the amplitude at the axis one obtains which is identical to the one derived on the basis of q-parameter for the x- component. The y- component is obtained in a similar way and the only difference is the index in (27) “x” which has to be replaced by “y”. After further elaborate calculations we find

(28)

where and are obtained from Eq.(22) and (23), respectively.

Lens systems consisting of more than one lens are used to modify the waist of a Gaussian beam. Systems consisting of two converging lenses or diverging and converging lenses are called the beam expander. The scheme of two converging lenses is shown in the Fig.2.

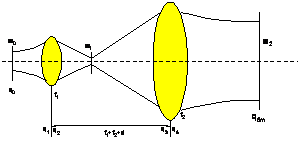
Fig.2 Two lens system

In investigation of two or more lens systems, the matrix method of forming transfer matrix is advisable. Matrix of the system is formed by the matrix product of the individual sections as explained earlier. For example, the matrix of the two-lens system is obtained from the product of three matrices:

(29)

where and are the focal lengths of the first and the second lens to which the beam is incident. Distance between the lenses is

If the beam waist is at the distance from the first lens then the q factors are:

, at the beam waist cross-section plane;

, at the cross-section plane in front of the first lens;

, at the cross-section after the first lens;

, at the cross-section of the beam waist after the first lens;

, at the cross-section before the second lens, and , at the cross-section of the output plane of the second lens.

The parameter is obtained from

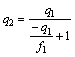(30)

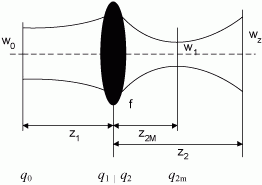
_{Fig. 3 Beam transformation through a lens}

The beam waist and its position after the first lens are obtained from , where . Hence,

, (31)

After substitution of defined parameters, we have also:

, (32)

To find beam waist and its position after the two lenses we have to use the matrix of the whole system as given by (1) so that

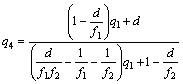(33)

To find the beam parameter after the second lens we have simply:. The new beam waist is obtained for a specific , where , i.e. the new beam waist after the system of two lenses is located at the plane where is imaginary. Since , the new beam waist is obtained from:

(34)

(35)

General solution of (34) and (35) is complex and will be given here in closed form only for effective magnification ratio:

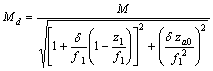(36)

where, is the maximum magnification, and .

In a special case when and the solution for (34) and (35) is simple:

, and (37)

This case is referred to as the astronomical beam expander if.

1. A. Marinčić,”Gausova funkcija u nekim problemima foton-elektronskih telekomunikacija“, Glas CCCXCV Srpske akademije nauka i umetnosti, Odeljenje tehničkih nauka, knj. 34-2003.
2. M. Born, E. Wolf, “Principles of Optics”, Pergamon Press, Oxford, Third Ed., 1965.
3. H. A. Haus, ”Waves and Fields in Optoelectronics”, Prentice Hall, Oxford, New Jersey, 1984.
4. A. Marinčić, B. Milovanović, “The three-dimensional Gaussian beam field in the focal region”, PES, 2005, Niš.
5. A. Marinčić,: ‘Huygens-Kirchhoff’s Theory in Calculation of Elliptical Gaussian Beam Propagation Through a Lens’, XXXVII Intern.Scientific Conference ICEST 2002, Oct.2002, Niš.